R

時系列解析の勉強2

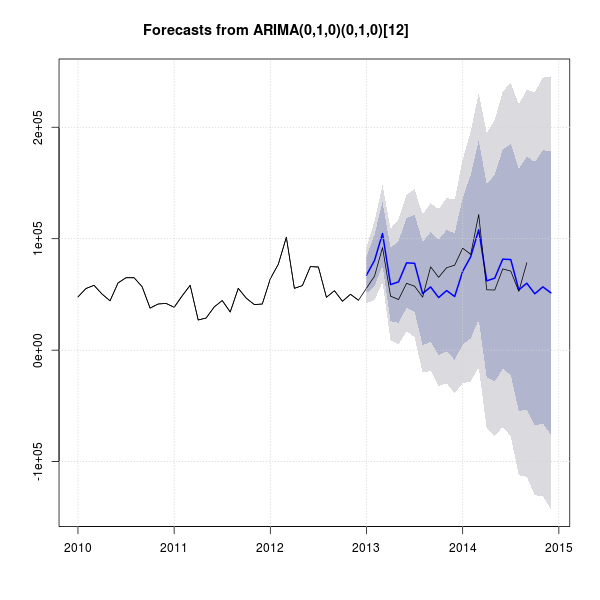
forecast、tseries、timsac

（とても勉強になったサイト）
logics of blue

データはホンダHPから入手。
手入力した部分もあるので間違いがあるかもしれません。

1
2
3
#HONDA <- read.table("clipboard", header=TRUE, sep="\t", na.strings="NA", dec=".", strip.white=TRUE)
#honda<-ts(HONDA, frequency =12, start = c(2010,1))
#save(honda,file="honda.dat")

honda.datを作業ディレクトリへ保存

読み込んでグラフ化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
load("honda.dat")
#項目ごとに分ける
dp<-honda[,1]
op<-honda[,2]
sales<-honda[,3]
export<-honda[,4]
#png("honda01.png", width =600, height =600)  # 描画デバイスを開く
par(mar=c(5,5,5,6),las=1,cex.axis=0.9,family="TakaoMincho")
ts.plot(dp,op,sales,export,gpars=list(xlab="年",ylab="台数",lty=c(1:4),col=c(1:4)),main="HONDA 2010.01_2014.09")
#legend("topleft",c("国内生産","海外生産","国内販売","輸出"),lty=c(1:4),col=c(1:4))
#axis(4,honda[nrow(honda),], c("国内生産","海外生産","国内販売","輸出"))
#最後のデータの国内生産と国内販売がほぼ同じ->個別にずらして描く
axis(4,honda[nrow(honda),1], label=F)
axis(4,honda[nrow(honda),1]-5000, "国内生産",col.axis=1,col="white")
axis(4,honda[nrow(honda),2], "海外生産",col.axis=2)
axis(4,honda[nrow(honda),3], label=F)
axis(4,honda[nrow(honda),3]+5000, "国内販売",col.axis=3,col="white")
axis(4,honda[nrow(honda),4], "輸出",col.axis=4)
grid()
#dev.off()

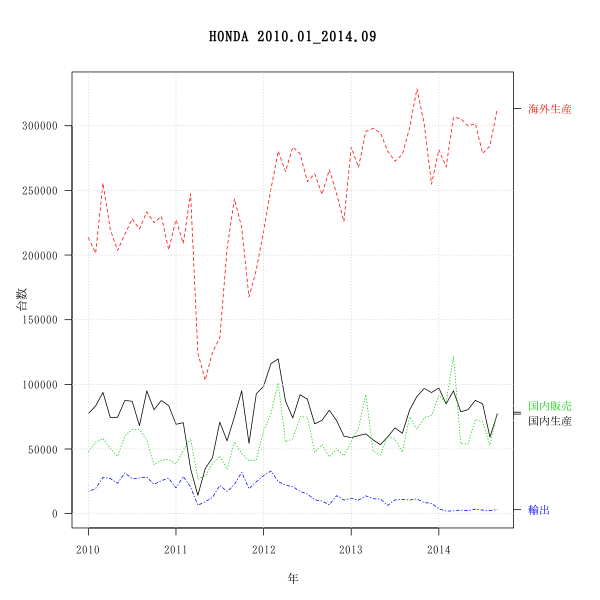
使用するパッケージ

1
2
3
library(forecast)
library(tseries)
library(timsac)
1
2
3
4
5
6
#国内販売(sales)を取り上げて分析
data<-sales
#時系列データを分析する際には、まずデータの変動がランダムウォークで表現できるか否か
#単位根検定 Phillips-Perron検定
#p値が0.05以下だと帰無仮説棄却（定常過程という判定）
PP.test(data)

Phillips-Perron Unit Root Test

data: data
Dickey-Fuller = -5.0908, Truncation lag parameter = 3, p-value = 0.01 

1
2
#DF検定
adf.test(data,k=0)

Augmented Dickey-Fuller Test

data: data
Dickey-Fuller = -5.1195, Lag order = 0, p-value = 0.01
alternative hypothesis: stationary 

1
2
#ADF検定 AR(p)過程まで守備範囲
adf.test(data)

Augmented Dickey-Fuller Test

data: data
Dickey-Fuller = -2.8843, Lag order = 3, p-value = 0.2179
alternative hypothesis: stationary 

1
2
3
4
5
6
7
tsdisplay(data)
#スペクトル
spectrum(data,method="ar")
#成分の分解
xt.sales<-stl(data,s.window="periodic")
plot(xt.sales)
decomp(data)

出力は省略

1
2
3
4
5
6
7
8
9
#2010_2012までのデータを作ってモデルを作り当てはまり具合を見る
nd <- window(data,end=c(2012,12))
# ホルト・ウィンタース法（汎用的な時系列モデル）
fit<-HoltWinters(nd,gamma=0) 
#png("honda02.png",width =600,height =600)
plot(forecast(fit,h=24))
lines(data)
grid()
#dev.off()

1
2
3
4
5
#SARIMA
(fit<-auto.arima(nd,trace=T,stepwise=F,approximation=F,start.p=0,
  start.q=0,start.P=0,start.Q=0))
#モデルの診断　作成したモデルの適切さを判断するためには、残差分析が必要
Box.test(fit$residuals)

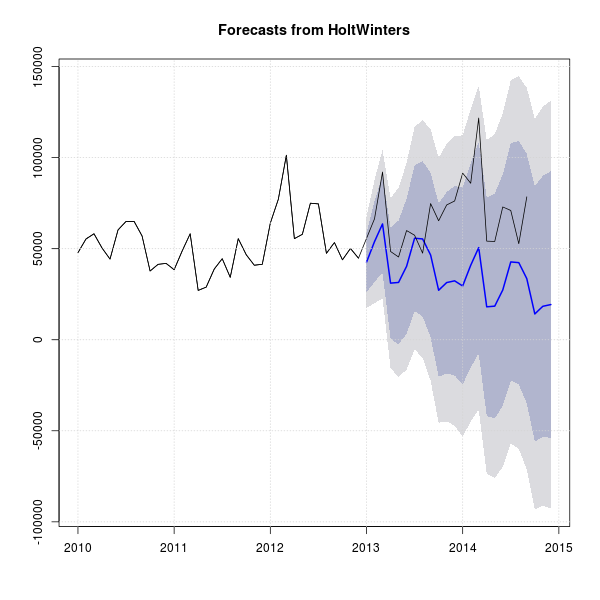
Box-Pierce test

data: fit$residuals
X-squared = 0.2984, df = 1, p-value = 0.5849

残差が独立である仮説が採択される

1
jarque.bera.test(fit$residuals)

Jarque Bera Test

data: fit$residuals
X-squared = 4.7357, df = 2, p-value = 0.09368

有意水準が5%でも帰無仮説は保留され (p > 0.05)、データは正規性をもつと判断できる。

1
2
3
#png("honda03.png",width =600,height =600)
tsdiag(fit)
#dev.off()

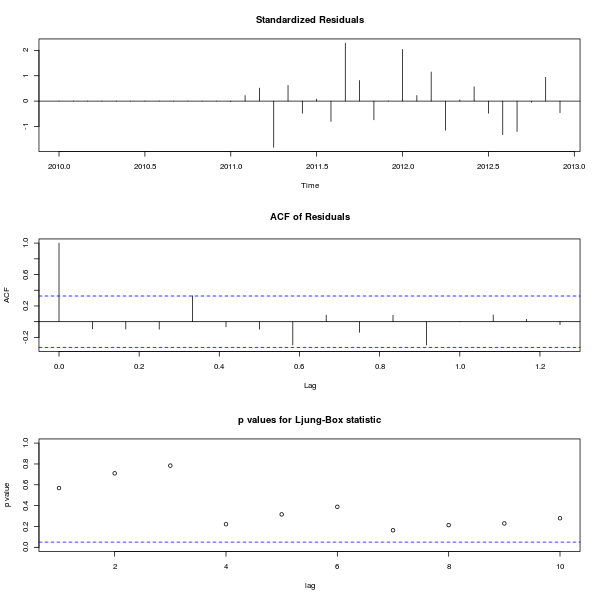
  • １番上が残差のプロット。２番目が残差の自己相関。これはなるべく小さい方がよい。
  • ３番目が残差が「ホワイトノイズ」になっているかの検定プロット。
  • 丸い点が上の方にあって、青い線を下回らないようであれば、ホワイトノイズと見なすこ とができる。
1
2
3
4
5
#png("honda04.png",width =600,height =600)
plot(forecast(fit,h=24))
lines(data)
grid()
#dev.off()