R

Rで計測震度の算出

Rで計測震度

（参考）
計測震度の算出方法
サンプルデータ 強震波形（平成12年(2000年)鳥取県西部地震） 米子市博労町
pdfファイル
計測震度の計算方法
プログラム
ソフトウェアのページ - 立命館大学 気象庁震度階の計算
（注）「まだ少し実測震度と0.1ほど誤差がある場合もあるようですが．．．」との事

計測震度( instrumental seismic intensity)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
isi <- function(df,fs) {
k<-nrow(df)
x<-df[,1];y<-df[,2];z<-df[,3]
num <- 2
while( num < k ) num <- num*2
xx<-numeric(num);yy<-numeric(num);zz<-numeric(num)
xx[1:k] <- x[1:k];yy[1:k] <- y[1:k];zz[1:k] <- z[1:k]
n <- 0:(num-1) # 時間軸
f <- n/(num/fs)+0.00000001 # 周波数軸
# フィルターの作成 
# 周期効果フィルター用の関数窓を作成
winX = sqrt(1.0/f)
# ハイカットフィルター用の関数窓を作成
y = f/10.0
winY = 1.0/sqrt(1.0 + 0.694*y^2 + 0.241*y^4+ 0.0557*y^6+ 0.009664*y^8+ 0.00134*y^10+ 0.000155*y^12)
# ローカットフィルター用の関数窓を作成
winZ = sqrt(1.0 - exp(-(f/0.5)^3))
# ３つの関数窓を合成
win1 = winX * winY * winZ
win2=rev(winX)*rev(winY)*rev(winZ)
win=c(win1[1:(num/2)],win2[(num/2+1):num])
#フーリエ変換
specxx = fft(xx);specyy = fft(yy);speczz = fft(zz)
# スペクトルにフィルターをかける
spec_winxx = win*specxx 
spec_winyy = win*specyy 
spec_winzz = win*speczz 
# フィルターをかけたスペクトルを逆フーリエ変換して時系列の波形に戻す
resxx=fft(spec_winxx,inverse =T)/num
resyy=fft(spec_winyy,inverse =T)/num
reszz=fft(spec_winzz,inverse =T)/num
# 3成分のベクトル合成波形の絶対値を求める。
S2 = abs(sqrt(resxx^2 + resyy^2+ reszz^2))
# 合成波形データを降順でソートして、地震加速度の大きい方から数えて「floor(0.3*fs)」個目の加速度から地震計の計測震度を求める
maxS2 = S2[order(S2,decreasing = TRUE )]
I = 2*log10(maxS2[floor(0.3*fs)]) + 0.94
#計測震度:計算されたIの小数第３位を四捨五入し、小数第２位を切り捨てたもの
I=floor(10*(I+0.005))/10 #小数第３位を四捨五入し、小数第２位を切り捨て
return(I)
}

米子市博労町 ５強 5.1のデータを読み込んで結果が一致するか確認

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
seibu<-read.csv("http://www.data.jma.go.jp/svd/eqev/data/kyoshin/jishin/001006_tottori-seibu/dat/AA06EA01.csv",skip=6,header=T)
I<-isi(seibu[1:2^13,],100)
#気象庁震度階級
if (I < 0.5){
sprintf("%s %1.1f","震度 0 計測震度:",I)
} else if ((I>=0.5) && (I <1.5)) {
sprintf("%s %1.1f","震度 1 計測震度:",I)
} else if ((I>=1.5) && (I <2.5)) {
sprintf("%s %1.1f","震度 2 計測震度:",I)
} else if ((I>=2.5) && (I <3.5)) {
sprintf("%s %1.1f","震度 3 計測震度:",I)
} else if ((I>=3.5) && (I <4.5)) {
sprintf("%s %1.1f","震度 4 計測震度:",I)
} else if ((I>=4.5) && (I <5.0)) {
sprintf("%s %1.1f","震度 5弱 計測震度:",I)
} else if ((I>=5.0) && (I <5.5)) {
sprintf("%s %1.1f","震度 5強 計測震度:",I)
} else if ((I>=5.5) && (I <6.0)) {
sprintf("%s %1.1f","震度 6弱 計測震度:",I)
} else if ((I>=6.0) && (I <6.5)) {
sprintf("%s %1.1f","震度 6強 計測震度:",I)
} else if (I>=6.5) {
sprintf("%s %1.1f","震度 7 計測震度:",I)
}

“震度 5強 計測震度: 5.1” (結果が一致した)



関数作成の備忘録

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#2^13=8192　個のデータを用いる
NS<-seibu$NS[1:2^13]
EW<-seibu$EW[1:2^13]
UD<-seibu$UD[1:2^13]
fs=100
num<-2^13
n <- 0:(num-1) # 時間軸
f <- n/(num/fs)+0.00000001 # 周波数軸
EW<-EW-mean(EW);NS<-NS-mean(NS);UD<-UD-mean(UD)
par(mfrow=c(3,1))
plot(n/fs,NS,type="l")
plot(n/fs,EW,type="l")
plot(n/fs,UD,type="l")
par(mfrow=c(1,1))

図は省略

1
2
3
4
5
6
7
8
9
# フーリエ変換
specEW = fft(EW)
specNS = fft(NS)
specUD = fft(UD)
par(mfrow=c(3,1))
plot(n/fs,abs(specNS),type="l",xlim=c(0,fs/2))
plot(n/fs,abs(specEW),type="l",xlim=c(0,fs/2))
plot(n/fs,abs(specUD),type="l",xlim=c(0,fs/2))
par(mfrow=c(1,1))

図は省略

フィルターの作成（はまった！！)

ポイントは「ナイキスト周波数」を境にしてかけるフィルターを変える

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 周期効果フィルター用の関数窓を作成
winX = sqrt(1/f)
# ハイカットフィルター用の関数窓を作成
y = f/10
winY = 1/sqrt(1 + 0.694*y^2 + 0.241*y^4+ 0.0557*y^6+ 0.009664*y^8+ 0.00134*y^10+ 0.000155*y^12)
# ローカットフィルター用の関数窓を作成
winZ = sqrt(1 - exp(-(f/0.5)^3))
# ３つの関数窓を合成
win1 = winX * winY * winZ
#nyquist=fs/2 より後はwin1はNG
#win1フィルターをかけると計測震度が4.6にしかならない
#win2:逆順にして掛けあわせ
win2=rev(winX)*rev(winY)*rev(winZ)
#win:やっと計測震度が一致した！
win=c(win1[1:(num/2)],win2[(num/2+1):num])

震度計算のための「フィルター特性グラフ」

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#png("isi01.png",width=1000,height=800)
gridx=c(seq(0.01,0.09,0.01),seq(0.1,0.9,0.1),seq(1,9,1),seq(10,100,10))
gridy=c(seq(1e-5,9e-5,1e-5),seq(1e-4,9e-4,1e-4),seq(0.001,0.009,0.001),seq(0.01,0.09,0.01),seq(0.1,0.9,0.1),seq(1,9,1),seq(10,100,10))
par(family="TakaoPMincho")
plot(f,winX,type="l",log="xy",xlim=c(0.01,100),ylim=c(1e-5,100),col="green",lwd=2,xlab="周波数(Hz)",ylab="補正係数",xaxt="n",yaxt="n",
panel.first = abline(v=gridx,h=gridy,col="lightgray",lty ="dotted"))
axis(1,c(0.01,0.1,1,10,100),
c("0.01","0.1","1","10","100"),las=1) 
axis(2,c(1e-5,1e-4,1e-3,0.01,0.1,1,10,100),
c("1e-5","1e-4","1e-3","0.01","0.1","1","10","100"),las=1) 
lines(f,winY,col="red",lwd=2)
lines(f,winZ,col="blue",lwd=2)
lines(f,win1,col="black",lwd=2)
title("震度計算のためのフィルター特性")
legend(
"topright",
c("Low cut","High cut","周期効果","総合"),
col = c("blue","red","green","black"),
lty = 1,
lwd = 2,
bg = "white"
)
#dev.off()

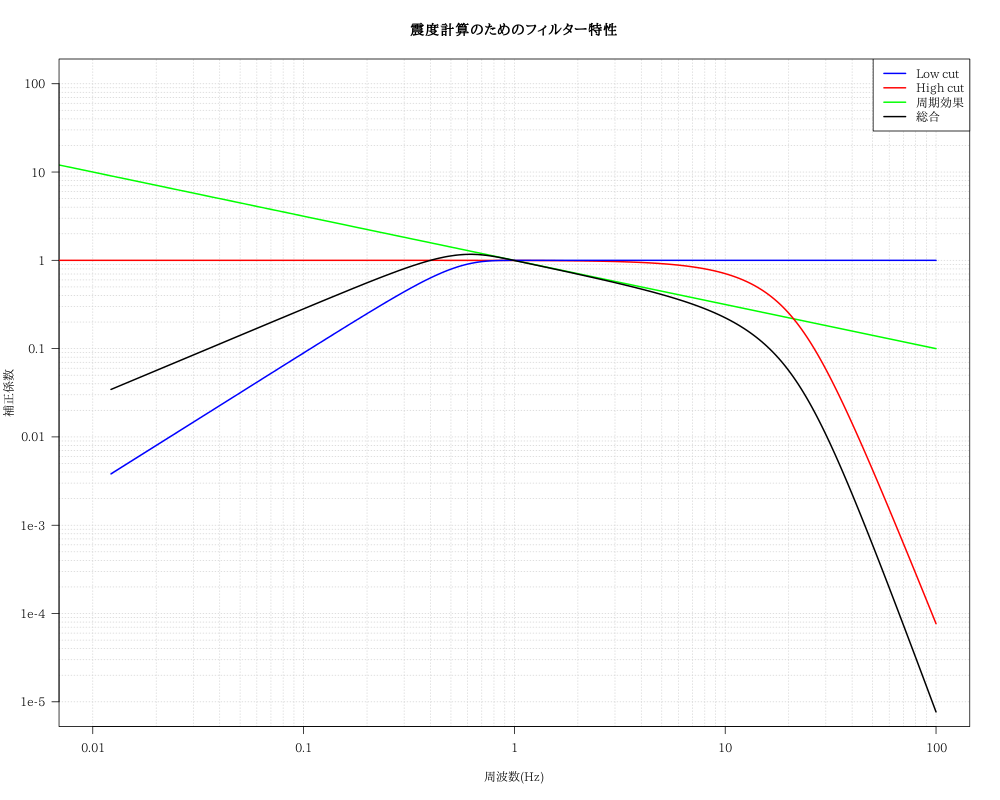
震度計算のためのフィルター(実際にかけるフィルター)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#png("isi02.png",width=1000,height=800)
gridx=c(seq(10,100,10))
gridy=c(seq(1e-5,9e-5,1e-5),seq(1e-4,9e-4,1e-4),seq(0.001,0.009,0.001),seq(0.01,0.09,0.01),seq(0.1,0.9,0.1),seq(1,9,1),seq(10,100,10))
par(family="TakaoPMincho")
plot(f,win2,type="l",log="y",xlim=c(0.01,100),ylim=c(1e-5,100),col="green",lwd=1,xlab="周波数(Hz)",ylab="補正係数",xaxt="n",yaxt="n",
panel.first = abline(v=gridx,h=gridy,col="lightgray",lty ="dotted"))
axis(1,seq(0,100,10),las=1) 
axis(2,c(1e-5,1e-4,1e-3,0.01,0.1,1,10,100),
c("1e-5","1e-4","1e-3","0.01","0.1","1","10","100"),las=1) 
lines(f,win1,col="red",lwd=1)
lines(f,win,col="blue",lwd=2,lty=3)
title("震度計算のためのフィルター")
legend(
"topright",
c("震度計算のためのフィルター","～nyquist","nyquist～"),
col = c("blue","red","green"),
lty = c(3,1,1),
lwd = c(2,1,1),
bg = "white"
)
#dev.off()

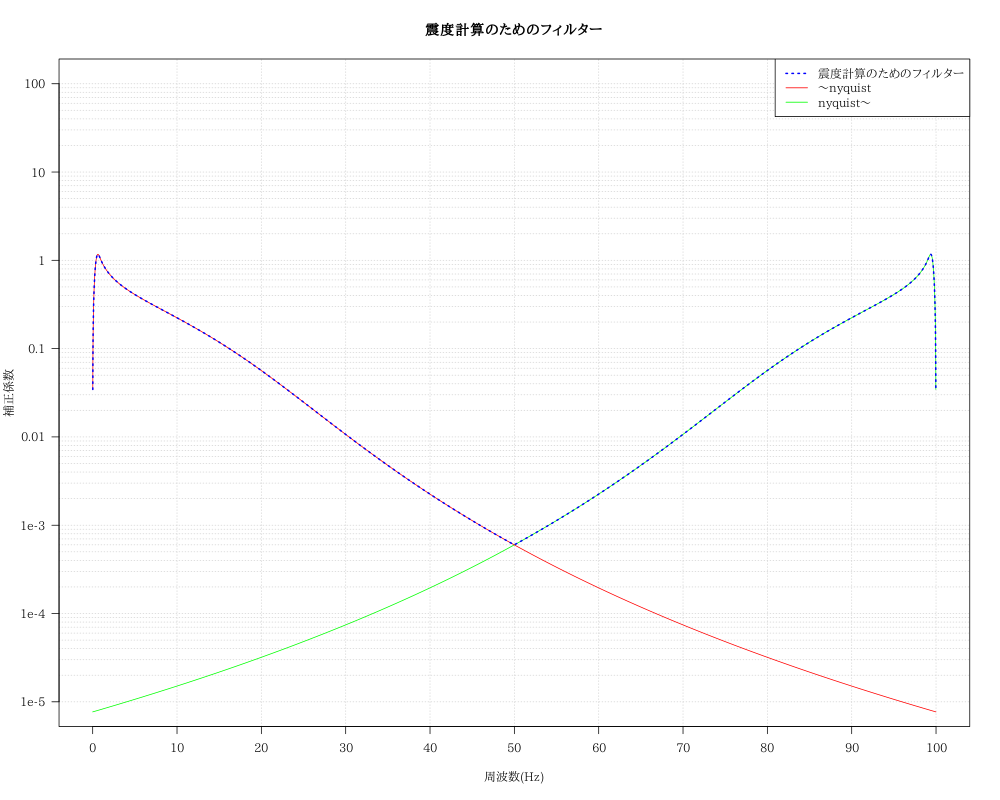
点線の部分をかける。ナイキスト周波数(この場合50Hz)に対して線対称

これで計測震度の算出方法のグラフとほぼ一致。

スペクトルにフィルターをかける

1
2
3
4
5
6
7
8
9
10
spec_winNS = win*specNS
spec_winEW = win*specEW
spec_winUD = win*specUD
#png("isi03.png",width=1000,height=800)
par(mfrow=c(3,1))
plot(f,spec_winNS,type="l")
plot(f,spec_winEW,type="l")
plot(f,spec_winUD,type="l")
par(mfrow=c(1,1))
#dev.off()

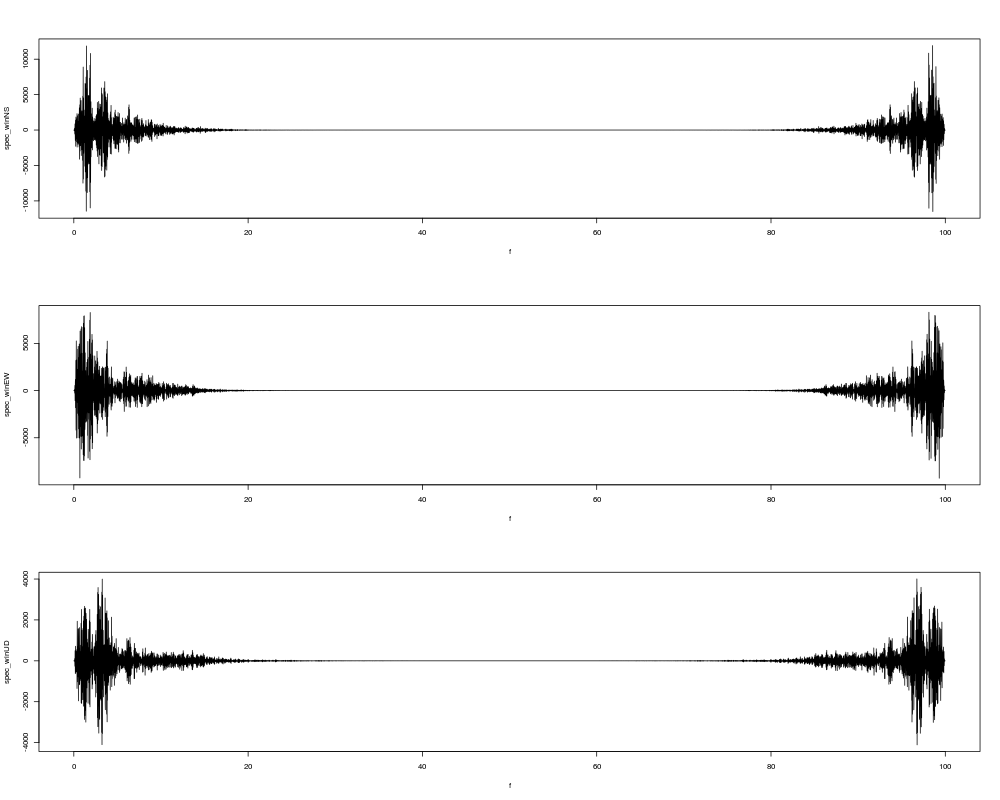
フィルター補正後の加速度波形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#pracmaパッケージのifft関数
#library("pracma")
#resEW=ifft(spec_winEW)
#resNS=ifft(spec_winNS)
#resUD=ifft(spec_winUD)
resEW=fft(spec_winEW,inverse =T)/num
resNS=fft(spec_winNS,inverse =T)/num
resUD=fft(spec_winUD,inverse =T)/num
#png("isi04.png",width=1000,height=800)
par(mfrow=c(3,1))
plot(n/fs,resNS,type="l")
plot(n/fs,resEW,type="l")
plot(n/fs,resUD,type="l")
par(mfrow=c(1,1))
#dev.off()

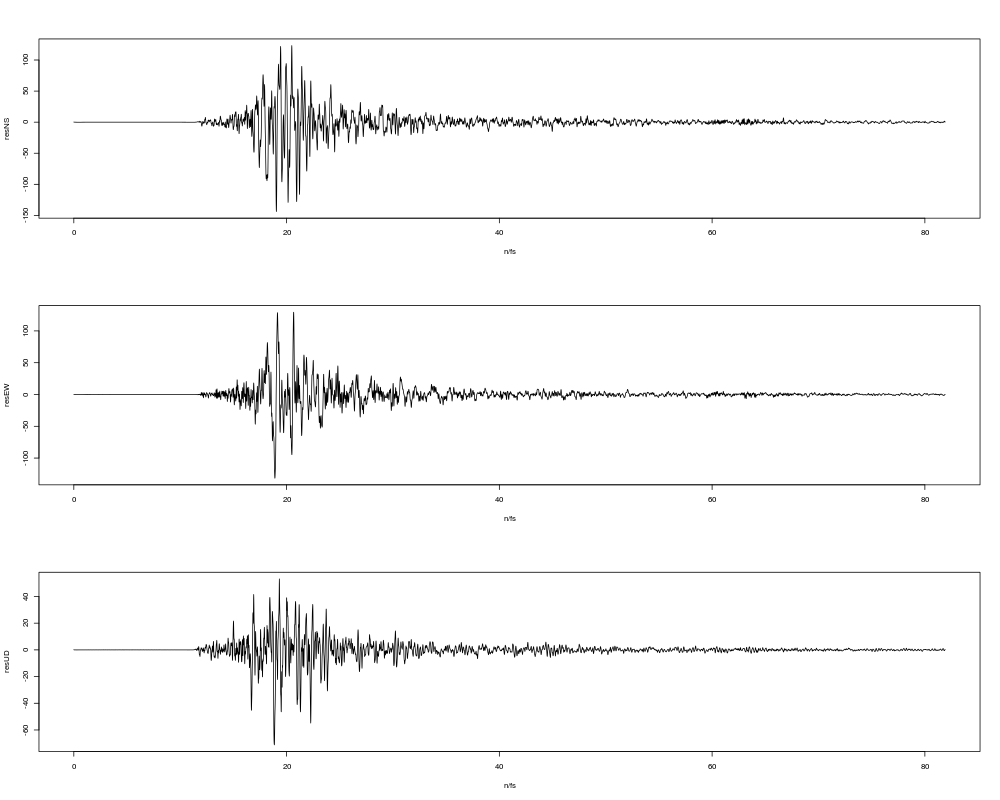
フィルター後の３成分合成加速度

1
2
3
4
S2 = abs(sqrt(resEW^2 + resNS^2 + resUD^2))
#png("isi05.png",width=1000,height=800)
plot(n/fs,S2,type="l")
#dev.off()

合成波形データを降順でソート
地震加速度の大きい方から数えて「floor(0.3*fs)」個目の加速度から地震計の計測震度を求める

1
2
3
4
maxS2 = S2[order(S2,decreasing = TRUE )]
I = 2*log10(maxS2[floor(0.3*fs)]) + 0.94
#計測震度:計算されたIの小数第３位を四捨五入し、小数第２位を切り捨てたもの
(I=floor(10*(I+0.005))/10) #小数第３位を四捨五入し、小数第２位を切り捨て

[1] 5.1