放送大学

組み合わせ計画法

第12章 組み合わせ計画法

p.160 最小木問題

igraphパッケージのminimum.spanning.treeを使う
この関数のアルゴリズムはプリム法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
library(igraph)
#エッジリストの作成
d <- data.frame(matrix(c( "1","2", "1","3", "1","4", "1","5", "2","3", "2","4", "4", "5"),nc=2,byrow=TRUE),stringsAsFactors=FALSE)
#ノードリストの作成
vers <- data.frame(c("1","2","3","4","5"),stringsAsFactors=FALSE)
#グラフの作成
#無向グラフ(directed=F)
g <- graph.data.frame(d,directed=F,vertices=vers)
#ウエイトの指定
E(g)$weight <- c(1,4,5,3,2,6,7)
V(g)$size <-35
#ノードの座標の指定
v1<- c(1,2); v2 <- c(2,3); v3 <- c(3,3); v4 <- c(3,1); v5 <- c(2,1)
lay <- rbind(v1,v2,v3,v4,v5)
mst <- minimum.spanning.tree(g)
#プロット
par(mfrow=c(1,2))
plot(g,layout=lay,vertex.label=V(g)$name,edge.label=E(g)$weight)
plot(mst,layout=lay,vertex.label=V(mst)$name,edge.label=E(mst)$weight)
par(mfrow=c(1,1))

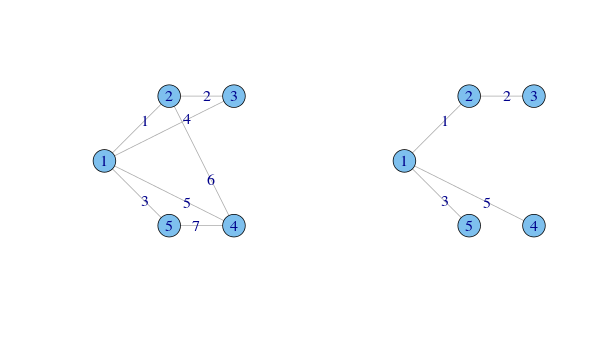
RBGLパッケージのmstree.kruskal関数はクラスカル法を使う。
このパッケージにはプリム法を使うmstree.prim関数も含まれる。
CRANには今のところ登録されていないのでインストールにちょっと手間がかかる。試行錯誤してやっとうまくできた。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#source("http://bioconductor.org/biocLite.R")
#biocLite("RBGL")
library(graph)
library(igraph)
library(RBGL)
d <- data.frame(matrix(c( "1","2", "1","3", "1","4", "1","5", "2","3", "2","4", "4", "5"),nc=2,byrow=TRUE),stringsAsFactors=FALSE)
weight <- c(1,4,5,3,2,6,7)
df<-as.data.frame(cbind(d,weight))
adjMST<-ftM2adjM(as.matrix(df[,1:2]),W=df[,3],edgemode="undirected")
dist.g<-as(adjMST,Class="graphNEL")
gg<-mstree.kruskal(dist.g)
#Compute minimum spanning tree for an undirected graph
#gg<-mstree.prim(g1)
gg1<- data.frame(cbind(t(gg$edgeList),t(gg$weight)))
#convert back to igraph package
mstKruskal <- graph.data.frame(gg1,directed=FALSE)
#ノードの座標の指定
v1<- c(1,2); v2 <- c(2,3); v3 <- c(3,3); v4 <- c(3,1); v5 <- c(2,1)
#ノード3とノード4の順番が入れ替わってしまったのでレイアウトの指定順も入れ替えた。
lay <- rbind(v1,v2,v4,v3,v5)
plot(mstKruskal, layout = lay,vertex.label=V(mstKruskal)$name,edge.label=E(mstKruskal)$weight)

p.164 ナップサック問題

1
2
3
4
5
6
7
8
9
10
library("adagio")
library(knitr)
profit<- c(9,7,6,5,3)
weight<- c(6,4,5,3,3)
table<-cbind(profit,weight)
row.names(table)<-c("1","2","3","4","5")
kable(table,row.names =T)
capacity <- 17
#0-1 Knapsack Problem
(is <- knapsack(w=weight, p=profit, cap=capacity))
profit weight
1 9 6
2 7 4
3 6 5
4 5 3
5 3 3

$capacity
[1] 16

$profit
[1] 24

$indices
[1] 1 2 4 5