Oct 5 2014

階層分析法

第7章階層分析法

群馬大青木先生の関数を読み込む。

1	source("http://aoki2.si.gunma-u.ac.jp/R/src/AHP.R", encoding="euc-jp")

AHP関数を使うと固有ベクトル法で分析できるが、ここでは問題解決の数理サイトのように過程をふみながら分析してみる。
Webサイトのweight関数とCI関数を合体させたweight_ci関数を作成。読み込む。

weight_ci <- function(A) {
  n <- ncol(A)
  w <- rep(1, n)
  sum <- 0
  for (i in 1:n) {
    for (j in 1:n) {
      w[i] <- w[i] * A[i, j]
    }
    w[i] <- w[i]^(1/n)
    sum <- sum + w[i]
  }
  for (i in 1:n) {
    w[i] <- w[i] / sum
  }
  L <- Re(eigen(A)$values)[1]
  CI <- (L - n) / (n - 1) # consistency index
    list(weight=w, CI=CI)
}

青木先生のAHP関数のラベル付けと行列の計算だけを残したAhp関数を作成。読み込む。

Ahp <- function(	x,	
			y,			
			labels.x=NULL,				# 評価基準のラベル
			labels.y=NULL)				# 代替案のラベル
{
	if (is.null(labels.x)) {				# ラベルが与えられていないときは A, B, ...
		labels.x <- LETTERS[1:length(x)]
	}
	names(x$weight) <- labels.x
	nitems.y <- nrow(y)
	if (is.null(labels.y)) {				# ラベルが与えられていないときは a, b, ...
		labels.y <- letters[1:nitems.y]
	}
	rownames(y) <- labels.y
	colnames(y) <- labels.x
	score <- rowSums(t(x$weight*t(y)))		# スコア
	return(structure(list(weight.x=x$weight, weight.y=y, score=score, sorted.score=sort(score)), class="AHP"))
}

分析する。

評価基準の一対比較行列を入力し、C.I.値と重要度を算出。
評価基準1～3に関して代替案の一対比較行列を入力、C.I.値と重要度を算出。
代替案の総合評価
青木先生の関数を使って評価を書き出し、かつ視覚化する。

x<-weight_ci(matrix(c(1,7,3, 1/7,1,1/3, 1/3,3,1), ncol=3, byrow=T))
x
Atime <- weight_ci(matrix(c(1,5,7,  1/5,1,5,  1/7,1/5,1), ncol=3, byrow=T))
Atime
Aclean <- weight_ci(matrix(c(1,1/5,1/3,  5,1,3,  3,1/3,1), ncol=3, byrow=T))
Aclean
Arent <- weight_ci(matrix(c(1,1/3,1/7,  3,1,1/5,  7,5,1), ncol=3, byrow=T))
Arent
y<-cbind(Atime$weight,Aclean$weight,Arent$weight)
y
res<-Ahp(x,y, labels.x=c("所要時間", "きれいさ", "家賃"), labels.y=c("代替案1", "代替案2", "代替案3"))
print(res)
plot(res)

x<-weight_ci(matrix(c(1,7,3, 1/7,1,1/3, 1/3,3,1), ncol=3, byrow=T))
x

$weight
[1] 0.66941687 0.08794621 0.24263692

$CI
[1] 0.003510883

Atime <- weight_ci(matrix(c(1,5,7, 1/5,1,5, 1/7,1/5,1), ncol=3, byrow=T))
Atime

$weight
[1] 0.71470956 0.21849437 0.06679607

$CI
[1] 0.0913834

Aclean <- weight_ci(matrix(c(1,1/5,1/3, 5,1,3, 3,1/3,1), ncol=3, byrow=T))
Aclean

$weight
[1] 0.1047294 0.6369856 0.2582850

$CI
[1] 0.01925555

Arent <- weight_ci(matrix(c(1,1/3,1/7, 3,1,1/5, 7,5,1), ncol=3, byrow=T))
Arent

$weight
[1] 0.08096123 0.18839410 0.73064467

$CI
[1] 0.03244379

y<-cbind(Atime$weight,Aclean$weight,Arent$weight)
y

0.71470956 0.1047294 0.08096123
0.21849437 0.6369856 0.18839410
0.06679607 0.2582850 0.73064467

res<-Ahp(x,y, labels.x=c(“所要時間”, “きれいさ”, “家賃”), labels.y=c(“代替案1”, “代替案2”, “代替案3”))
print(res)

評価基準の重み

所要時間きれいさ家賃
0.66942 0.08795 0.24264

代替案の評価結果

所要時間きれいさ家賃
代替案1 0.71471 0.10473 0.08096
代替案2 0.21849 0.63699 0.18839
代替案3 0.06680 0.25828 0.73064

スコア

代替案1 代替案2 代替案3
0.50729 0.24800 0.24471

ソートされたスコア

代替案3 代替案2 代替案1
0.24471 0.24800 0.50729

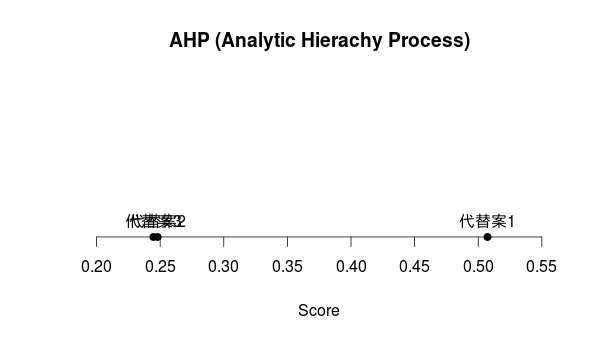
青木先生のAHP関数を使う。

1
2
3

res2<-AHP(c(1/7,1/3,3),cbind(c(1/5,1/7,1/5),c(5,3,1/3),c(3,7,5)), labels.x=c("所要時間", "きれいさ", "家賃"), labels.y=c("代替案1", "代替案2", "代替案3"))
print(res2)
plot(res2)

第7章 階層分析法

第7章階層分析法