放送大学

最大流問題

問題解決の数理 第4章 ネットワーク計画法2

線形計画問題として解く

最大化

$$\begin{aligned} &f=x_{12}+x_{13} \end{aligned}$$

制約条件

$$\begin{aligned} &x_{24}+x_{25}-x_{12}=0\\ &x_{34}+x_{36}-x_{13}=0\\ &x_{47}-x_{24}-x_{34}=0\\ &x_{57}-x_{25}=0\\ &x_{67}-x_{36}=0\\ &0\leq x_{12}\leq3\\ &0\leq x_{13}\leq5\\ &0\leq x_{24}\leq2\\ &0\leq x_{25}\leq2\\ &0\leq x_{34}\leq3\\ &0\leq x_{36}\leq3\\ &0\leq x_{47}\leq2\\ &0\leq x_{57}\leq3\\ &0\leq x_{67}\leq4\\ \end{aligned}$$

表にしてみた

枝 1->2 1->3 2->4 2->5 3->4 3->6 4->7 5->7 6->7 符号 rhs
最大化 1 1 0 0 0 0 0 0 0
点2 -1 0 1 1 0 0 0 0 0 == 0
点3 0 -1 0 0 1 1 0 0 0 == 0
点4 0 0 -1 0 -1 0 1 0 0 == 0
点5 0 0 0 -1 0 0 0 1 0 == 0
点6 0 0 0 0 0 -1 0 0 1 == 0
容量制約 1 0 0 0 0 0 0 0 0 <= 3
容量制約 0 1 0 0 0 0 0 0 0 <= 5
容量制約 0 0 1 0 0 0 0 0 0 <= 2
容量制約 0 0 0 1 0 0 0 0 0 <= 2
容量制約 0 0 0 0 1 0 0 0 0 <= 3
容量制約 0 0 0 0 0 1 0 0 0 <= 3
容量制約 0 0 0 0 0 0 1 0 0 <= 2
容量制約 0 0 0 0 0 0 0 1 0 <= 3
容量制約 0 0 0 0 0 0 0 0 1 <= 4

Rglpk_solve_LP関数（Rglpkパッケージ）を使う

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
library("Rglpk")
obj <- c(1,1,0,0,0,0,0,0,0)
mat <- rbind(
c(-1,0,1,1,0,0,0,0,0),
c(0,-1,0,0,1,1,0,0,0),
c(0,0,-1,0,-1,0,1,0,0),
c(0,0,0,-1,0,0,0,1,0),
c(0,0,0,0,0,-1,0,0,1),
c(1,0,0,0,0,0,0,0,0),
c(0,1,0,0,0,0,0,0,0),
c(0,0,1,0,0,0,0,0,0),
c(0,0,0,1,0,0,0,0,0),
c(0,0,0,0,1,0,0,0,0),
c(0,0,0,0,0,1,0,0,0),
c(0,0,0,0,0,0,1,0,0),
c(0,0,0,0,0,0,0,1,0),
c(0,0,0,0,0,0,0,0,1))
dir <- c("==","==","==","==","==","<=","<=","<=","<=","<=","<=","<=","<=","<=")
rhs <- c(0,0,0,0,0,3,5,2,2,3,3,2,3,4)
max <- T
Rglpk_solve_LP(obj, mat, dir, rhs, max = max)

$optimum
7

$solution
3 4 1 2 1 3 2 2 3

$status
0

igraphパッケージを使う

1
2
3
4
5
6
library(igraph)
E <- rbind( c(1,2,3), c(1,3,5), c(2,5,2), c(2,4,2), c(3,4,3), c(3,6,3),c(4,7,2),c(5,7,3),c(6,7,4))
colnames(E) <- c("from", "to", "capacity")
g <- graph.data.frame(as.data.frame(E))
V(g)$size <-30
plot(g,vertex.label=V(g)$name,edge.label=E(g)$capacity)

1
2
3
4
5
6
#p.60
v1<- c(1,2); v2 <- c(2,3); v3 <- c(2,1); v4 <- c(3,2); v5 <- c(4,3); v6 <- c(4,1);v7<-c(5,2)
lay <- rbind(v1,v2,v3,v4,v5,v6,v7)
#プロット
V(g)$size <-30
plot(g,layout=lay,vertex.label=V(g)$name,edge.label=E(g)$capacity)

1
2
3
4
5
6
7
res<-graph.maxflow(g, source=V(g)["1"], target=V(g)["7"])
V(g)$size <-30
V(g)$shape <- "circle"  #形状
V(g)$shape[1] <- "square" ;V(g)$shape[7] <- "square"
V(g)$color <- "skyblue"  #色
V(g)$color[1] <- "pink" ;V(g)$color[7] <- "pink"
plot(g,layout=lay,vertex.label=V(g)$name,edge.label=res$flow)

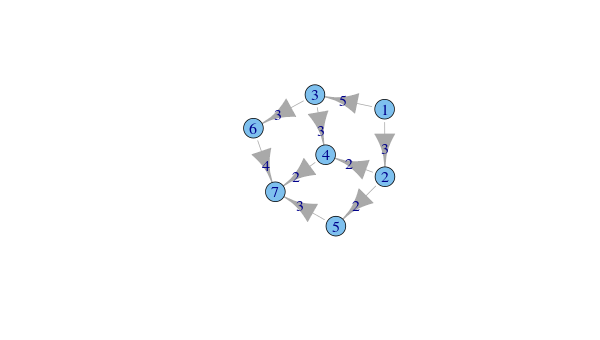
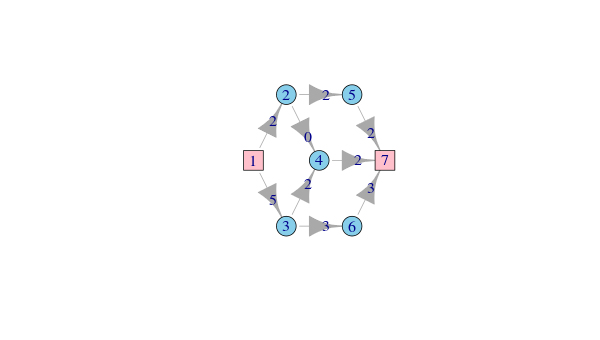
Rglpk_solve_LP関数を使って解いた解とは別の解になっている