放送大学

クラスター分析（１）

階層的クラスター

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
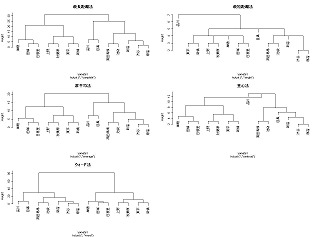
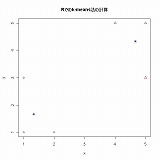
品川<-c(0,7,12,14,18,22,25,28,24,21,17,14,10,7)
目黒<-c(7,0,5,7,11,15,18,23,31,28,24,21,17,14)
渋谷<-c(12,5,0,2,6,10,13,18,22,25,29,26,22,19)
原宿<-c(14,7,2,0,4,8,11,16,20,23,27,28,24,21)
新宿<-c(18,11,6,4,0,4,7,12,16,19,23,26,28,25)
高田馬場<-c(22,15,10,8,4,0,3,8,12,15,19,22,26,29)
池袋<-c(25,18,13,11,7,3,0,5,9,12,16,19,23,26)
巣鴨<-c(28,23,18,16,12,8,5,0,4,7,11,14,18,21)
田端<-c(24,31,22,20,16,12,9,4,0,3,7,10,14,17)
日暮里<-c(21,28,25,23,19,15,12,7,3,0,4,7,11,14)
上野<-c(17,24,29,27,23,19,16,11,7,4,0,3,7,10)
秋葉原<-c(14,21,26,28,26,22,19,14,10,7,3,0,4,7)
東京<-c(10,17,22,24,28,26,23,18,14,11,7,4,0,3)
新橋<-c(7,14,19,21,25,29,26,21,17,14,10,7,3,0)
d<-data.frame(品川,目黒,渋谷,原宿,新宿,高田馬場,池袋,巣鴨,田端,日暮里,上野,秋葉原,東京,新橋)
row.names(d)<-c("品川","目黒","渋谷","原宿","新宿","高田馬場","池袋","巣鴨","田端","日暮里","上野","秋葉原","東京","新橋")
yamate0<-as.matrix(d)
yamate1<-as.dist(yamate0)
par(mfrow=c(3,2))
yamate4<-hclust(yamate1)
plot(yamate4,main="最長距離法")
yamate4<-hclust(yamate1,method="single")
plot(yamate4,main="最短距離法")
yamate4<-hclust(yamate1,method="average")
plot(yamate4,main="群平均法")
yamate4<-hclust(yamate1,method="centroid")
plot(yamate4,main="重心法")
yamate4<-hclust(yamate1,method="ward")
plot(yamate4,main="ウォード法")
par(mfrow=c(1,1))

k-means法

1
2
3
4
5
6
7
x<-c(1,2,1,4,5,5)
y<-c(1,1,3,5,5,3)
d<-data.frame(x,y)
row.names(d)<-c("C1","C2","C3","C4","C5","C6")
km1<-as.matrix(d)
km2<-kmeans(km1,2)
km2

K-means clustering with 2 clusters of sizes 3, 3

Cluster means:
x y
1 1.333333 1.666667
2 4.666667 4.333333

Clustering vector:
C1 C2 C3 C4 C5 C6
1 1 1 2 2 2

Within cluster sum of squares by cluster:
3.333333 3.333333
(between_SS / total_SS = 80.4 %)

Available components:

“cluster” “centers” “totss” “withinss” “tot.withinss” “betweenss” “size” “iter” “ifault” 

1
2
plot(km1,pch=km2$cluster,col=km2$cluster,main="Rでのk-means法の計算")
points(km2$centers,pch=8,col="blue")