放送大学

心理統計法('17) その6

放送大学「心理統計法(‘17)」第10章 その１

授業ではrstanパッケージを使ってますが、MCMCpackパッケージを使ってみます。初学者ですので間違いが多々あると思います。

（Rスクリプトはここ）
早稲田大学文学部文学研究科 豊田研究室

（参考）
ベイジアンMCMCによる統計モデル
Using the ggmcmc package
Bayesian Inference With Stan ~番外編~
Exercise 2: Bayesian A/B testing using MCMC Metropolis-Hastings
政治学方法論 I

1
2
3
library(MCMCpack)
library(knitr)
#library(loo)

推測例１（交互作用の分析）

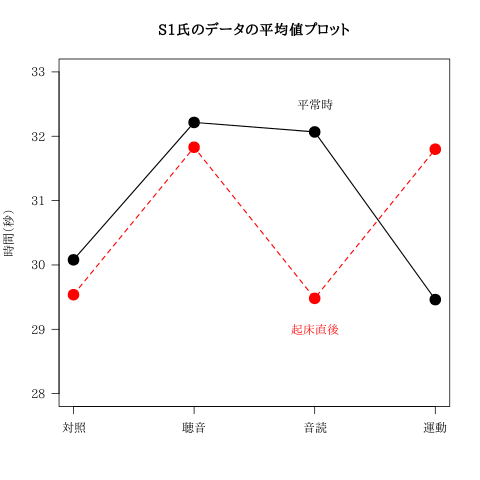
表10.1「知覚時間」データ入力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
y1<-c(
   28.10,31.67,33.60,25.37,32.03,32.21,29.62,29.69,29.65,28.86,
   31.35,30.10,30.64,32.65,34.80,32.24,31.27,30.31,30.49,38.30,
   33.32,31.82,31.94,34.10,31.34,29.52,34.38,30.54,32.96,30.75,
   33.95,30.16,29.60,30.10,27.39,28.50,26.07,28.08,30.59,30.18,
   34.48,28.44,28.95,30.33,28.61,28.68,28.34,28.00,29.74,29.81,
   28.17,31.10,29.84,30.06,32.11,33.85,36.45,30.64,36.35,29.72,
   29.58,34.12,27.92,26.39,27.98,32.27,25.27,31.28,31.19,28.81,
   31.92,30.81,31.02,33.46,36.87,31.53,28.56,30.16,32.52,31.14)
A <- rep(1:4,each=10,times=2)       #要因Aの水準の指定
B <- rep(1:2,each=40)               #要因Bの水準の指定
#
#mat<-matrix(c(mean(y1[1:10]), mean(y1[11:20]),mean(y1[21:30]),mean(y1[31:40]),
#	mean(y1[41:50]),mean(y1[51:60]),mean(y1[61:70]),mean(y1[71:80]) ),ncol=2,byrow=F)
dat<-data.frame(A,B,y1)
Data<-split(dat,list(dat$A,dat$B))
mat <- matrix(apply(sapply(Data, "[[", 3),2,mean),ncol=2,byrow=F)
#
#
#
#png("sinri10_01.png")
par(family="TakaoPMincho")
matplot(1:4, mat, type="l", ylab="時間（秒）", xlab="",main="S1氏のデータの平均値プロット", lwd=1.5,col=1:2, xaxt = "n",las=1,ylim=c(28,33))
matplot(1:4, mat, type="p", ylab="", xlab="",main="", pch=19,cex=2, col=1:2,xaxt = "n",ylim=c(28,33),add=T)
axis(1,1:4,labels=c("対照","聴音","音読","運動"))
text(x=3,y=32.5,labels="平常時",col=1)
text(x=3,y=29,labels="起床直後",col=2)
#dev.off()

1
2
3
4
5
6
7
8
9
#mean_sd<-matrix(c(mean(y1[1:10]), mean(y1[11:20]),mean(y1[21:30]),mean(y1[31:40]),
#	mean(y1[41:50]),mean(y1[51:60]),mean(y1[61:70]),mean(y1[71:80]) ),ncol=8)
#mean_sd<-rbind(mean_sd,matrix(c(sqrt(9/10)*sd(y1[1:10]), sqrt(9/10)*sd(y1[11:20]),sqrt(9/10)*sd(y1[21:30]),sqrt(9/10)*sd(y1[31:40]),
#	sqrt(9/10)*sd(y1[41:50]),sqrt(9/10)*sd(y1[51:60]),sqrt(9/10)*sd(y1[61:70]),sqrt(9/10)*sd(y1[71:80]) ),ncol=8) )
mean_sd <- matrix(apply(sapply(Data, "[[", 3),2,mean),ncol=8)
mean_sd <- rbind(mean_sd,matrix(apply(sapply(Data, "[[", 3),2,sd)*sqrt(9/10),ncol=8) )
colnames(mean_sd)<-c("平常時 対照","平常時 聴音","平常時 音読","平常時 運動","起床直後 対照","起床直後 聴音","起床直後 音読","起床直後 運動")
rownames(mean_sd)<-c("平均","標準偏差")
kable(round(mean_sd,2))
平常時 対照 平常時 聴音 平常時 音読 平常時 運動 起床直後 対照 起床直後 聴音 起床直後 音読 起床直後 運動
平均 30.08 32.21 32.07 29.46 29.54 31.83 29.48 31.8
標準偏差 2.27 2.43 1.52 2.04 1.79 2.70 2.61 2.1 
1
kable(t(round(mean_sd,2)))
平均 標準偏差
平常時 対照 30.08 2.27
平常時 聴音 32.21 2.43
平常時 音読 32.07 1.52
平常時 運動 29.46 2.04
起床直後 対照 29.54 1.79
起床直後 聴音 31.83 2.70
起床直後 音読 29.48 2.61
起床直後 運動 31.80 2.10 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
fun <- function(beta, x1 , x2 , x3 , x4 ,x5 ,x6,x7,x8) {
#  mu : beta[1]  
#  a1 : beta[2] , a2 : beta[3] , a3 : beta[4]  
#  b1 : beta[5]  
#  ab11 : beta[6] , ab21 : beta[7] , ab31 : beta[8] 
#  sigmaE : beta[9] 
## a4  :  -(beta[2]+beta[3]+beta[4])  
## b2  :  -beta[5]
## ab12 : -beta[6]  ,                  ab22 : -beta[7] ,             ab32 : -beta[8] , 
## ab41 : -(beta[6]+beta[7]+beta[8]) , ab42 : beta[6]+beta[7]+beta[8]
	ifelse( beta[9] < 0  , l<- -Inf ,
### mu + a + b + (ab) + sigmaE
	l <-    sum(log(dnorm(x1, mean=beta[1] +beta[2]                      +beta[5]    +beta[6]                    , sd=beta[9]))  ) +	# a1 , b1
		sum(log(dnorm(x2, mean=beta[1] +beta[3]                      +beta[5]    +beta[7]                    , sd=beta[9]))  ) +	# a2 , b1
		sum(log(dnorm(x3, mean=beta[1] +beta[4]                      +beta[5]    +beta[8]                    , sd=beta[9]))  ) +	# a3 , b1
		sum(log(dnorm(x4, mean=beta[1] +(-(beta[2]+beta[3]+beta[4])) +beta[5]    +(-(beta[6]+beta[7]+beta[8])), sd=beta[9]))  ) +	# a4 , b1
		sum(log(dnorm(x5, mean=beta[1] +beta[2]                      +(-beta[5]) +(-beta[6])                  , sd=beta[9]))  ) +	# a1 , b2
		sum(log(dnorm(x6, mean=beta[1] +beta[3]                      +(-beta[5]) +(-beta[7])                  , sd=beta[9]))  ) +	# a2 , b2
		sum(log(dnorm(x7, mean=beta[1] +beta[4]                      +(-beta[5]) +(-beta[8])                  , sd=beta[9]))  ) +	# a3 , b2
		sum(log(dnorm(x8, mean=beta[1] +(-(beta[2]+beta[3]+beta[4])) +(-beta[5]) +(beta[6]+beta[7]+beta[8])   , sd=beta[9]))  )) 	# a4 , b2
	return(l)
}
#
chains  <- 1:5
seeds  <- seq(1,5,1)
init<-c(1,1,1,1,1,1,1,1,30)
burnin<-2000
mcmc_n<-200000
thin<- verbose <-10
#sink("./likelihood.txt")
E2Ind<- lapply(chains ,
			function(chain) {
				MCMCmetrop1R(fun = fun ,
				theta.init = init ,
				burnin = burnin, mcmc = mcmc_n ,thin=thin,
#				verbose= verbose,
				seed = seeds[chain],
				x1=y1[1:10], x2=y1[11:20],x3=y1[21:30],x4=y1[31:40],
				x5=y1[41:50],x6=y1[51:60],x7=y1[61:70],x8=y1[71:80] )})
# sink()
# system("gawk '/function value/' ./likelihood.txt | gawk 'gsub(\"function value =\",\"\")' > ./lik.txt")
# l<-scan("./lik.txt")
# ll<-matrix(l,ncol=length(chains),byrow = FALSE)
# head(ll) ; tail(ll)
# lll<-ll[-c(1 : burnin/thin),]
# ( waic1 <- waic(matrix(lll,ncol=1)) )
#
### waic         371.2
#
E2Ind.mcmc <- mcmc.list(E2Ind)
#
#summary(E2Ind.mcmc)
#
#gelman.diag(E2Ind.mcmc)
#
#effectiveSize(E2Ind.mcmc)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
df <- data.frame(mu=unlist(E2Ind.mcmc[,1]),muA1=unlist(E2Ind.mcmc[,2]) ,muA2=unlist(E2Ind.mcmc[,3]) ,muA3=unlist(E2Ind.mcmc[,4]) ,
	muA4= -(unlist(E2Ind.mcmc[,2])+unlist(E2Ind.mcmc[,3])+unlist(E2Ind.mcmc[,4])) ,
	muB1= (unlist(E2Ind.mcmc[,5]))  , muB2= -unlist(E2Ind.mcmc[,5]) ,
	muAB11 = unlist(E2Ind.mcmc[,6])  ,muAB12 = -unlist(E2Ind.mcmc[,6]),
	muAB21 = unlist(E2Ind.mcmc[,7]) , muAB22 = -unlist(E2Ind.mcmc[,7]),
	muAB31 = unlist(E2Ind.mcmc[,8]) , muAB32 = -unlist(E2Ind.mcmc[,8]) ,
	muAB41 = -(unlist(E2Ind.mcmc[,6]) + unlist(E2Ind.mcmc[,7]) + unlist(E2Ind.mcmc[,8])) , 
	muAB42 =  unlist(E2Ind.mcmc[,6]) + unlist(E2Ind.mcmc[,7]) + unlist(E2Ind.mcmc[,8]) ,
	sigmaE = unlist(E2Ind.mcmc[,9]) )
#
#ryou<-data.frame(c(round(mean(df[,1]),2) , round(sd(df[,1]),2) ,
#	round(quantile(df[,1],c(0.025,0.05,0.5,0.95,0.975)),2)))
#for (i in 2:ncol(df) ){
#ryou<-cbind(ryou,data.frame(c(round(mean(df[,i]),2) , round(sd(df[,i]),2) ,
#	round(quantile(df[,i],c(0.025,0.05,0.5,0.95,0.975)),2))))
#}
#names(ryou)<-c("mu","muA1","muA2","muA3","muA4","muB1","muB2","muAB11","muAB12","muAB21","muAB22","muAB31","muAB32","muAB41","muAB42","sigmaE")
#rownames(ryou)<-c("EAP","post.sd","2.5%","5%","50%","95%","97.5%")
#kable(t(ryou))
#
ryou<-rbind(EAP=apply(df, 2, mean),post.sd=apply(df, 2, sd),
apply(df, 2, quantile, probs=c(0.025,0.05, 0.5,0.95, 0.975)))
kable(t(round(ryou,2)))
EAP post.sd 2.5% 5% 50% 95% 97.5%
mu 30.81 0.26 30.29 30.37 30.81 31.24 31.33
muA1 -1.00 0.46 -1.92 -1.76 -1.00 -0.24 -0.10
muA2 1.21 0.46 0.30 0.45 1.21 1.97 2.12
muA3 -0.04 0.46 -0.94 -0.79 -0.04 0.72 0.87
muA4 -0.18 0.46 -1.08 -0.93 -0.18 0.58 0.73
muB1 0.15 0.27 -0.38 -0.30 0.15 0.59 0.67
muB2 -0.15 0.27 -0.67 -0.59 -0.15 0.30 0.38
muAB11 0.13 0.46 -0.78 -0.63 0.12 0.88 1.03
muAB12 -0.13 0.46 -1.03 -0.88 -0.12 0.63 0.78
muAB21 0.04 0.46 -0.86 -0.71 0.04 0.80 0.94
muAB22 -0.04 0.46 -0.94 -0.80 -0.04 0.71 0.86
muAB31 1.15 0.46 0.24 0.39 1.15 1.91 2.05
muAB32 -1.15 0.46 -2.05 -1.91 -1.15 -0.39 -0.24
muAB41 -1.32 0.46 -2.23 -2.08 -1.31 -0.55 -0.40
muAB42 1.32 0.46 0.40 0.55 1.31 2.08 2.23
sigmaE 2.37 0.20 2.02 2.07 2.36 2.73 2.81

水準とセルの効果の評価

P.147 (9.12)式

水準・交互作用の効果が０より大きい（小さい）確率

1
2
3
4
5
6
7
8
9
10
11
12
c0<-matrix(rep(NA,28),ncol=14)
colnames(c0)<-c("muA1","muA2","muA3","muA4","muB1","muB2","muAB11","muAB12","muAB21","muAB22","muAB31","muAB32","muAB41","muAB42")
rownames(c0)<-c("0 < ","=< 0")
#
c<-0
for (i in 2:15){
t<-sum((df[,i] > c)=="TRUE")
f<-sum((df[,i] < c)=="TRUE")
c0[1,i-1] <- round(t/ nrow(df),3)
c0[2,i-1] <- round(f/ nrow(df),3)
}
kable(c0)
muA1 muA2 muA3 muA4 muB1 muB2 muAB11 muAB12 muAB21 muAB22 muAB31 muAB32 muAB41 muAB42
0 < 0.016 0.995 0.47 0.348 0.71 0.29 0.609 0.391 0.538 0.462 0.993 0.007 0.002 0.998
=< 0 0.984 0.005 0.53 0.652 0.29 0.71 0.391 0.609 0.462 0.538 0.007 0.993 0.998 0.002

要因の効果の評価

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#### 測定値の標準偏差
#
sigmaA<-sqrt((df$muA1^2+  df$muA2^2 + df$muA3^2 + df$muA4^2)/4)
#sigmaB<-sqrt((df$muB1^2+  df$muB2^2)/2)
sigmaB<-sqrt(df$muB1^2)
sigmaAB<-sqrt((df$muAB11^2+  df$muAB12^2 + df$muAB21^2 + df$muAB22^2 + df$muAB31^2+  df$muAB32^2 + df$muAB41^2 + df$muAB42^2)/8)
#
#### 説明率
#
etaA2<-sigmaA^2/(sigmaA^2+sigmaB^2+sigmaAB^2+df$sigmaE^2)
etaB2<-sigmaB^2/(sigmaA^2+sigmaB^2+sigmaAB^2+df$sigmaE^2)
etaAB2<-sigmaAB^2/(sigmaA^2+sigmaB^2+sigmaAB^2+df$sigmaE^2)
etat2<-(sigmaA^2+sigmaB^2+sigmaAB^2)/(sigmaA^2+sigmaB^2+sigmaAB^2+df$sigmaE^2)
#
#### 効果量
#
deltaA<-sigmaA/df$sigmaE
deltaB<-sigmaB/df$sigmaE
deltaAB<-sigmaAB/df$sigmaE
#
hyouka<-cbind(sigmaA,sigmaB,sigmaAB,sigmaE=df$sigmaE,etaA2,etaB2,etaAB2,etat2,deltaA,deltaB,deltaAB)
#
#h<-data.frame(c(round(mean(hyouka[,1]),3) , round(sd(hyouka[,1]),3) ,
#	round(quantile(hyouka[,1],c(0.025,0.05,0.5,0.95,0.975)),3)))
#for (i in 2:ncol(hyouka) ){
#h<-cbind(h,data.frame(c(round(mean(hyouka[,i]),3) , round(sd(hyouka[,i]),3) ,
#	round(quantile(hyouka[,i],c(0.025,0.05,0.5,0.95,0.975)),3))))
#}
#rownames(h)<-c("EAP","post.sd","2.5%","5%","50%","95%","97.5%")
#names(h)<-c("sigmaA","sigmaB","sigmaAB","sigmaE","etaA2","etaB2","etaAB2","etat2","deltaA","deltaB","deltaAB")
#kable(t(h))
#
ryou<-rbind(EAP=apply(hyouka, 2, mean),post.sd=apply(hyouka, 2, sd),
apply(hyouka, 2, quantile, probs=c(0.025,0.05, 0.5,0.95, 0.975)))
kable(t(round(ryou,3)))
EAP post.sd 2.5% 5% 50% 95% 97.5%
sigmaA 0.880 0.251 0.398 0.471 0.876 1.299 1.386
sigmaB 0.245 0.183 0.010 0.019 0.208 0.595 0.678
sigmaAB 0.956 0.255 0.467 0.543 0.952 1.383 1.470
sigmaE 2.375 0.203 2.018 2.069 2.360 2.732 2.812
etaA2 0.109 0.053 0.022 0.031 0.104 0.205 0.226
etaB2 0.012 0.016 0.000 0.000 0.006 0.046 0.058
etaAB2 0.128 0.058 0.031 0.042 0.123 0.231 0.253
etat2 0.249 0.070 0.116 0.135 0.248 0.366 0.388
deltaA 0.373 0.108 0.164 0.196 0.371 0.553 0.589
deltaB 0.103 0.077 0.004 0.008 0.088 0.251 0.285
deltaAB 0.405 0.111 0.192 0.225 0.404 0.590 0.626

セル平均の事後分布

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
mu11<-df$mu + df$muA1 + df$muB1 + df$muAB11
mu12<-df$mu + df$muA1 + df$muB2 + df$muAB12
mu21<-df$mu + df$muA2 + df$muB1 + df$muAB21
mu22<-df$mu + df$muA2 + df$muB2 + df$muAB22
mu31<-df$mu + df$muA3 + df$muB1 + df$muAB31
mu32<-df$mu + df$muA3 + df$muB2 + df$muAB32
mu41<-df$mu + df$muA4 + df$muB1 + df$muAB41
mu42<-df$mu + df$muA4 + df$muB2 + df$muAB42
#
zigo<-cbind(mu11,mu12,mu21,mu22,mu31,mu32,mu41,mu42)
#
#z<-data.frame(c(round(mean(zigo[,1]),2) , round(sd(zigo[,1]),2) ,
#	round(quantile(zigo[,1],c(0.025,0.05,0.5,0.95,0.975)),2)))
#for (i in 2:ncol(zigo) ){
#z<-cbind(z,data.frame(c(round(mean(zigo[,i]),2) , round(sd(zigo[,i]),2) ,
#	round(quantile(zigo[,i],c(0.025,0.05,0.5,0.95,0.975)),2))))
#}
#rownames(z)<-c("EAP","post.sd","2.5%","5%","50%","95%","97.5%")
#names(z)<-c("mu11","mu12","mu21","mu22","mu31","mu32","mu41","mu42")
#kable(t(z))
#
ryou<-rbind(EAP=apply(zigo, 2, mean),post.sd=apply(zigo, 2, sd),
apply(zigo, 2, quantile, probs=c(0.025,0.05, 0.5,0.95, 0.975)))
kable(t(round(ryou,2)))
EAP post.sd 2.5% 5% 50% 95% 97.5%
mu11 30.08 0.76 28.59 28.84 30.08 31.32 31.57
mu12 29.54 0.75 28.07 28.31 29.54 30.78 31.02
mu21 32.21 0.75 30.74 30.98 32.21 33.44 33.68
mu22 31.83 0.75 30.35 30.60 31.83 33.07 33.32
mu31 32.07 0.75 30.59 30.83 32.07 33.31 33.56
mu32 29.48 0.75 28.01 28.25 29.48 30.72 30.97
mu41 29.46 0.76 27.98 28.22 29.46 30.69 30.95
mu42 31.80 0.75 30.31 30.56 31.80 33.04 33.28

セル平均mu_jkは、mu_j’k’より大きい

1
2
3
4
5
6
7
8
9
10
11
Umu_jk<-matrix(rep(NA,64),ncol=8)
colnames(Umu_jk)<-c("mu11","mu12","mu21","mu22","mu31","mu32","mu41","mu42")
rownames(Umu_jk)<-c("mu11","mu12","mu21","mu22","mu31","mu32","mu41","mu42")
#
for (i in 1:8){
	for (j in 1:8){
t<-sum((zigo[,i] - zigo[,j] > 0)=="TRUE")
Umu_jk[i,j] <- round(t/ nrow(zigo),3)
	}
}
kable(Umu_jk)
mu11 mu12 mu21 mu22 mu31 mu32 mu41 mu42
mu11 0.000 0.697 0.024 0.050 0.031 0.716 0.720 0.054
mu12 0.303 0.000 0.007 0.018 0.009 0.523 0.530 0.017
mu21 0.976 0.993 0.000 0.639 0.555 0.994 0.994 0.649
mu22 0.950 0.982 0.361 0.000 0.412 0.986 0.986 0.512
mu31 0.969 0.991 0.445 0.588 0.000 0.992 0.992 0.600
mu32 0.284 0.477 0.006 0.014 0.008 0.000 0.506 0.016
mu41 0.280 0.470 0.006 0.014 0.008 0.494 0.000 0.015
mu42 0.946 0.983 0.351 0.488 0.400 0.984 0.985 0.000

特に興味のある２セル間の比較

「音読」における「平常時」ー「起床直後」の差の推測

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
mu31_mu32<-mu31 - mu32
#summary(mu31_mu32)
#
#### 効果量 delta 
## P.130 (8.7)式
#
delta<-mu31_mu32/df$sigmaE
#summary(delta)
#
#### 非重複度
## P.96 (6.7)式
#
U3<-pnorm(mu31, mean =mu32, sd = df$sigmaE)
#summary(U3)
#
#### 優越率
## P.102 (6.18)式
#
pid<-pnorm(delta/sqrt(2) , mean =0, sd = 1)
#summary(pid)
#
#### 閾上率
## P.105 (6.24)式
#
c<-1
pi1<-pnorm( (mu31_mu32-c)/(sqrt(2)*df$sigmaE) , mean =0, sd = 1)
#summary(pi1)
#
hyouka31_32<-cbind(mu31_mu32,delta,U3,pid,pi1)
#
#h<-data.frame(c(round(mean(hyouka31_32[,1]),3) , round(sd(hyouka31_32[,1]),3) ,
#	round(quantile(hyouka31_32[,1],c(0.025,0.05,0.5,0.95,0.975)),3)))
#for (i in 2:ncol(hyouka31_32) ){
#h<-cbind(h,data.frame(c(round(mean(hyouka31_32[,i]),3) , round(sd(hyouka31_32[,i]),3) ,
#	round(quantile(hyouka31_32[,i],c(0.025,0.05,0.5,0.95,0.975)),3))))
#}
#rownames(h)<-c("EAP","post.sd","2.5%","5%","50%","95%","97.5%")
#names(h)<-c("mu31_mu32","delta","U3","pi_d","pi_1")
#kable(t(h))
#
ryou<-rbind(EAP=apply(hyouka31_32, 2, mean),post.sd=apply(hyouka31_32, 2, sd),
apply(hyouka31_32, 2, quantile, probs=c(0.025,0.05, 0.5,0.95, 0.975)))
kable(t(round(ryou,3)))
EAP post.sd 2.5% 5% 50% 95% 97.5%
mu31_mu32 2.587 1.068 0.485 0.843 2.584 4.344 4.688
delta 1.097 0.458 0.202 0.349 1.097 1.852 1.997
U3 0.841 0.105 0.580 0.636 0.864 0.968 0.977
pid 0.770 0.095 0.557 0.597 0.781 0.905 0.921
pi1 0.675 0.110 0.441 0.482 0.683 0.842 0.865

「起床直後」における「運動」ー「音読」の差の推測

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
mu42_mu32<-mu42 - mu32
#summary(mu42_mu32)
#
#### 効果量 delta 
## P.130 (8.7)式
#
delta<-mu42_mu32/df$sigmaE
#summary(delta)
#
#### 非重複度
## P.96 (6.7)式
#
U3<-pnorm(mu42, mean =mu32, sd = df$sigmaE)
#summary(U3)
#
#### 優越率
## P.102 (6.18)式
pid<-pnorm(delta/sqrt(2) , mean =0, sd = 1)
#summary(pid)
#
#### 閾上率
## P.105 (6.24)式
#
c<-1
pi1<-pnorm( (mu42_mu32-c)/(sqrt(2)*df$sigmaE) , mean =0, sd = 1)
#summary(pi1)
#
hyouka42_32<-cbind(mu42_mu32,delta,U3,pid,pi1)
#
#h<-data.frame(c(round(mean(hyouka42_32[,1]),3) , round(sd(hyouka42_32[,1]),3) ,
#	round(quantile(hyouka42_32[,1],c(0.025,0.05,0.5,0.95,0.975)),3)))
#for (i in 2:ncol(hyouka42_32) ){
#h<-cbind(h,data.frame(c(round(mean(hyouka42_32[,i]),3) , round(sd(hyouka42_32[,i]),3) ,
#	round(quantile(hyouka42_32[,i],c(0.025,0.05,0.5,0.95,0.975)),3))))
#}
#rownames(h)<-c("EAP","post.sd","2.5%","5%","50%","95%","97.5%")
#names(h)<-c("mu42_mu32","delta","U3","pi_d","pi_1")
#kable(t(h))
#
ryou<-rbind(EAP=apply(hyouka42_32, 2, mean),post.sd=apply(hyouka42_32, 2, sd),
apply(hyouka42_32, 2, quantile, probs=c(0.025,0.05, 0.5,0.95, 0.975)))
kable(t(round(ryou,3)))
EAP post.sd 2.5% 5% 50% 95% 97.5%
mu42_mu32 2.321 1.068 0.232 0.575 2.316 4.082 4.410
delta 0.984 0.456 0.096 0.239 0.982 1.735 1.876
U3 0.815 0.114 0.538 0.594 0.837 0.959 0.970
pid 0.746 0.099 0.527 0.567 0.756 0.890 0.908
pi1 0.647 0.113 0.410 0.450 0.653 0.821 0.846