時系列解析の勉強1

forecast、tseries、timsac

（とても勉強になったサイト）
logics of blue

使用するパッケージ

1
2
3

library(forecast)
library(tseries)
library(timsac)

ホワイトノイズを作成
自己相関がないのか確認
forecastパッケージのtsdisplay関数

1
2
3

set.seed(1)
white.noise <- rnorm(n=400)
tsdisplay(white.noise)

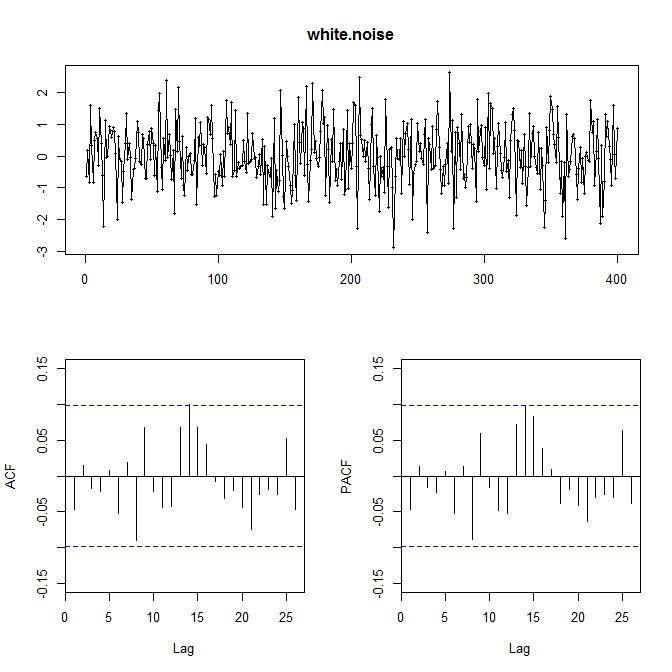
自己相関なし

単位根検定

1	adf.test(white.noise)

p-value = 0.01
(単位根なし。定常(時間や位置によって確率分布が変化しない確率過程)）

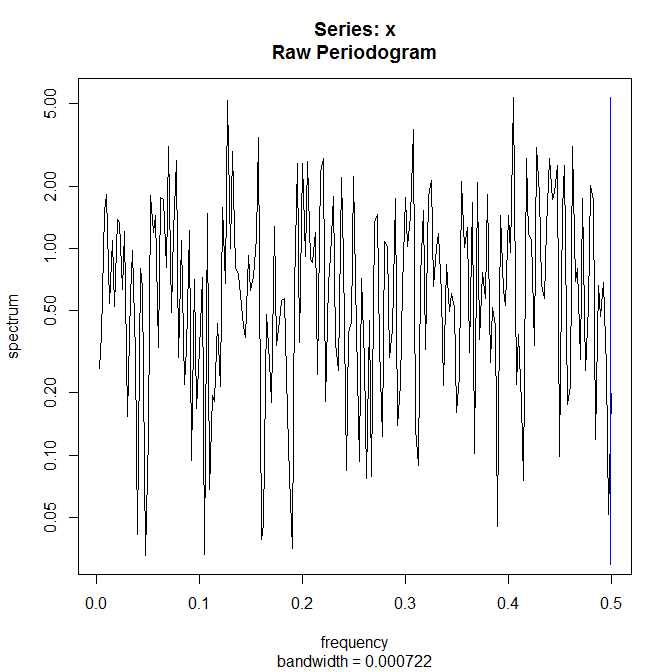
スペクトル

1	spectrum(white.noise)

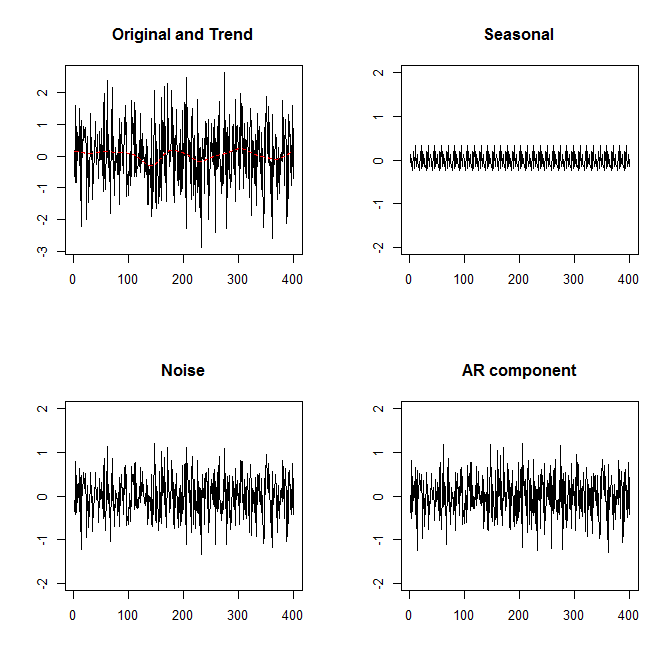
成分分解
（timsacパッケージのdecomp関数を使ってみます)

1	decomp(white.noise)

ホワイトノイズにARIMAモデルを適用するとしたらどんなモデルになるのか？
forecastパッケージのauto.arima関数

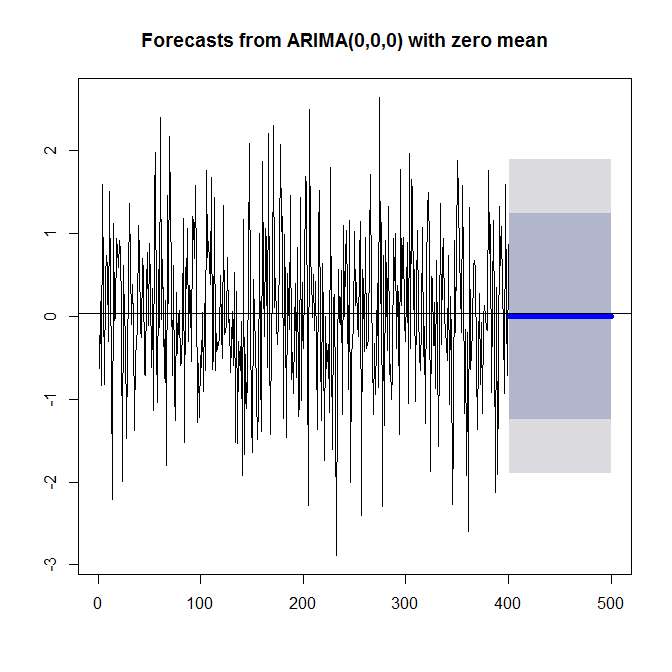
1	(model.noise <- auto.arima(white.noise,ic="aic",trace=T,stepwise=F,approximation=F))

選ばれたモデル

Series: white.noise
ARIMA(0,0,0) with zero mean

予測結果

1 2	plot(forecast(model.noise, h=100), flwd=5) abline(h=mean(white.noise))

ランダムウォークデータ作成(ホワイトノイズの累積和を取る)

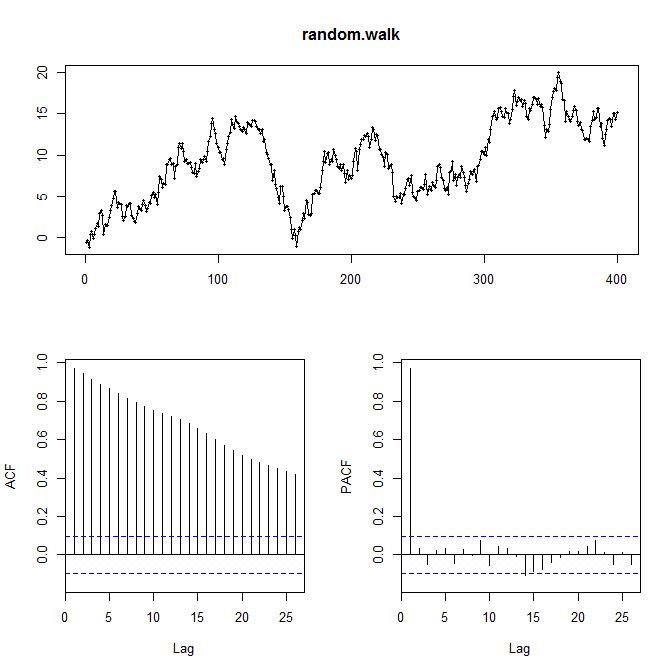
1 2	random.walk <- cumsum(white.noise) tsdisplay(random.walk)

ホワイトノイズと違って自己相関がある

単位根検定

1	adf.test(random.walk)

p-value = 0.3132
(単位根あり。定常ではない)

次に、差分をとって調べてみると

1	adf.test(diff(random.walk))

p-value = 0.01
(単位根なし。定常)

スペクトル

1	spectrum(random.walk)

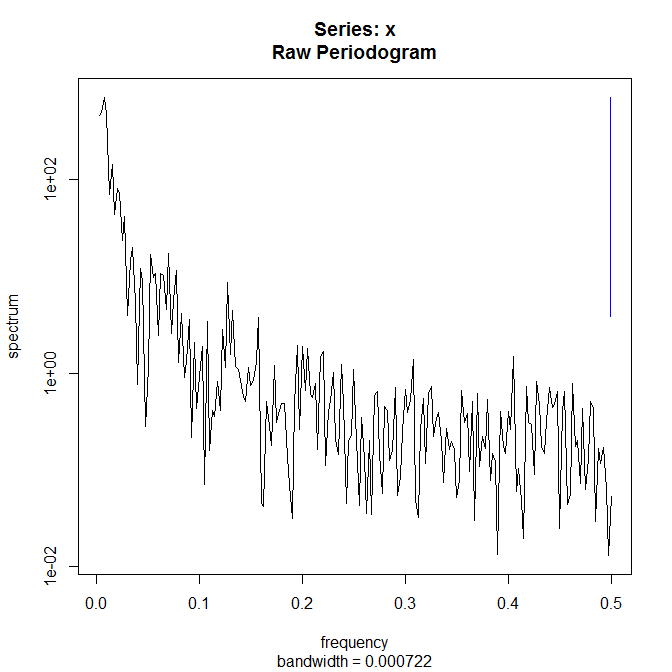
成分分解

1	decomp(random.walk)

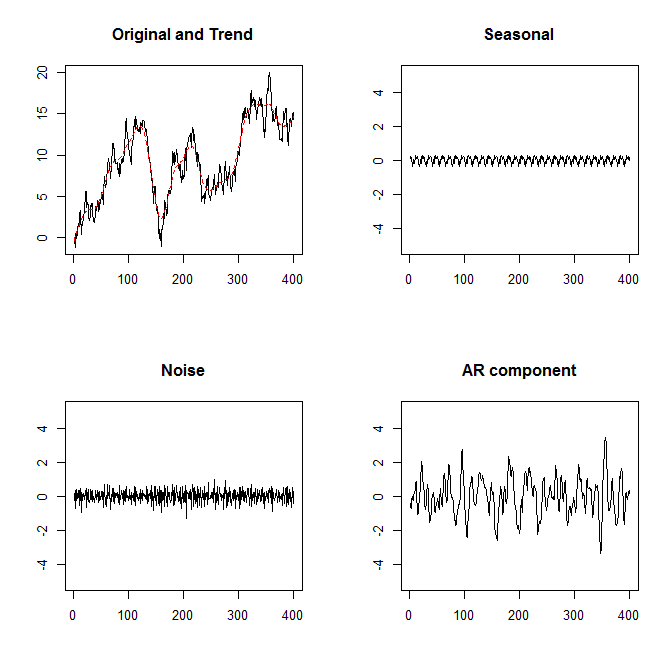
モデル選択

1	(model.rw<- auto.arima(random.walk,ic="aic",trace=T,stepwise=F,approximation=F))

Series: random.walk
ARIMA(0,1,0) with drift

上記サイトと違って with drift = ドリフト項（基本的な方向性）付きが選ばれた。

1
2
3

plot(forecast(model.rw, h=100), flwd=5)
abline(h=mean(random.walk))
abline(h=random.walk[400], col=2, lty=2)

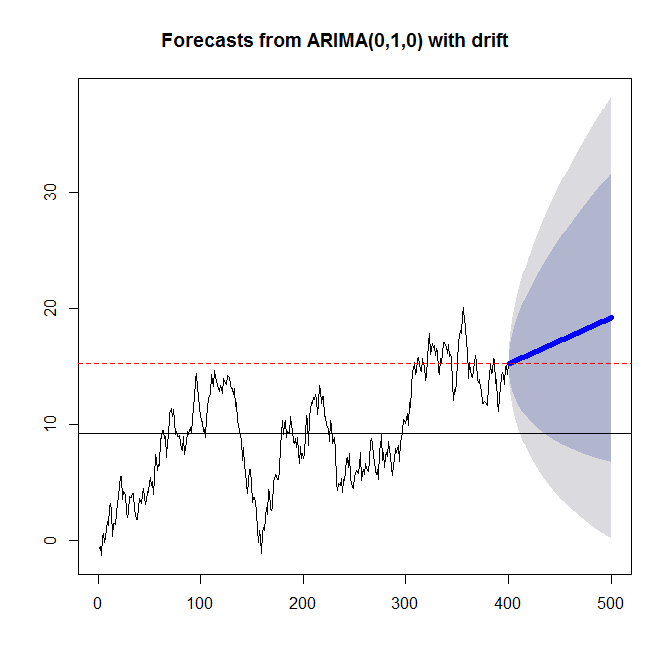
予測は「右肩上がりに線形に上昇」

(上記サイトより抜粋)
和分過程(階差を取れば定常になるときの原系列)ではない、定常過程ならば平均に回帰する。
（和分過程の例がランダムウォークで、定常過程の例がホワイトノイズ。）
予測をする際、データが和分過程かどうかで結果が相当変わってくる。