放送大学「心理統計法(‘17)」第14章
授業ではrstanパッケージを使ってますが、MCMCpackパッケージを使ってみます。初学者ですので間違いが多々あると思います。
(Rスクリプトはここ)
早稲田大学文学部文学研究科 豊田研究室
(参考)
ベイジアンMCMCによる統計モデル
Using the ggmcmc package
Bayesian Inference With Stan ~番外編~
Exercise 2: Bayesian A/B testing using MCMC Metropolis-Hastings
政治学方法論 I
(データ)豊田 秀樹, 前田 忠彦, 柳井 晴夫の原因をさぐる統計学―共分散構造分析入門 (ブルーバックス)より
演習用公開データ
|
|
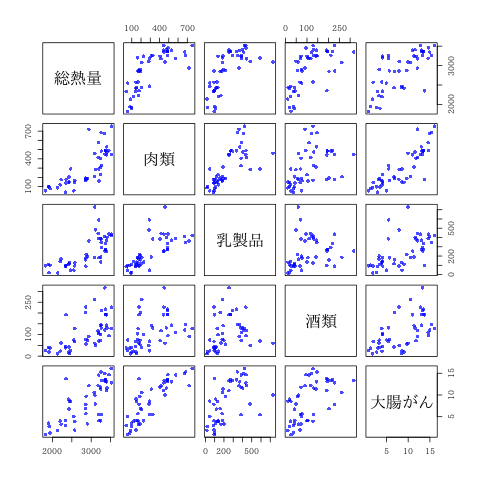
多変量散布図
|
|
共分散行列
Rのcov関数で求める共分散は標本共分散。(n-1 で割る)
それを考慮して
|
|
| 総熱量 | 肉類 | 乳製品 | 酒類 | 大腸がん | |
|---|---|---|---|---|---|
| 総熱量 | 250240 | 74906 | 57018 | 23564 | 1672 |
| 肉類 | 74906 | 37514 | 22301 | 6497 | 746 |
| 乳製品 | 57018 | 22301 | 25376 | 2747 | 417 |
| 酒類 | 23564 | 6497 | 2747 | 5518 | 197 |
| 大腸がん | 1672 | 746 | 417 | 197 | 20 |
平均・標準偏差・相関行列
平均
|
|
総熱量 肉類 乳製品 酒類 大腸がん
2871 307 243 109 9
標準偏差
|
|
総熱量 肉類 乳製品 酒類 大腸がん
500 194 159 74 5
相関行列
|
|
| 総熱量 | 肉類 | 乳製品 | 酒類 | 大腸がん | |
|---|---|---|---|---|---|
| 総熱量 | 1.000 | 0.773 | 0.716 | 0.634 | 0.739 |
| 肉類 | 0.773 | 1.000 | 0.723 | 0.452 | 0.853 |
| 乳製品 | 0.716 | 0.723 | 1.000 | 0.232 | 0.579 |
| 酒類 | 0.634 | 0.452 | 0.232 | 1.000 | 0.588 |
| 大腸がん | 0.739 | 0.853 | 0.579 | 0.588 | 1.000 |
予測変数を「総熱量」「肉類」「乳製品」「酒類」とし重回帰分析を行う
|
|
| EAP | post.sd | 2.5% | 5% | 50% | 95% | 97.5% | |
|---|---|---|---|---|---|---|---|
| a(切片) | 0.55361 | 2.99219 | -5.38977 | -4.36036 | 0.54635 | 5.47844 | 6.45255 |
| 総熱量(b1) | 0.00053 | 0.00143 | -0.00229 | -0.00181 | 0.00053 | 0.00288 | 0.00336 |
| 肉類(b2) | 0.01735 | 0.00301 | 0.01146 | 0.01240 | 0.01735 | 0.02228 | 0.02325 |
| 乳製品(b3) | -0.00153 | 0.00361 | -0.00867 | -0.00746 | -0.00151 | 0.00434 | 0.00553 |
| 酒類(b4) | 0.01383 | 0.00648 | 0.00107 | 0.00321 | 0.01382 | 0.02446 | 0.02662 |
| sigmaE(誤差sd) | 2.31097 | 0.26293 | 1.86597 | 1.92508 | 2.28665 | 2.78110 | 2.89779 |
「乳製品」の偏回帰係数(b3)のEAPが負の値になっているが、
|
|
0.5787253
予測変数の選択のためにヒストグラムを描いてみた
|
|
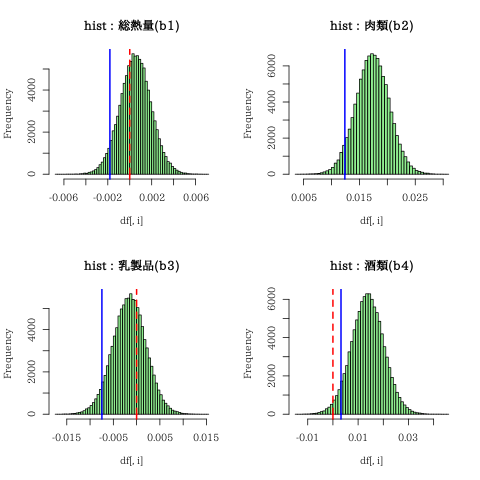
青線(5%)赤破線(0)の位置関係を見る
予測変数を「肉類」と「酒類」とし重回帰分析を再度行う。
|
|
| EAP | post.sd | 2.5% | 5% | 50% | 95% | 97.5% | |
|---|---|---|---|---|---|---|---|
| a(切片) | 1.566 | 0.685 | 0.217 | 0.440 | 1.566 | 2.692 | 2.917 |
| 肉類(b2) | 0.017 | 0.002 | 0.013 | 0.014 | 0.017 | 0.020 | 0.021 |
| 酒類(b4) | 0.016 | 0.005 | 0.006 | 0.007 | 0.016 | 0.024 | 0.025 |
| sigmaE(誤差sd) | 2.263 | 0.252 | 1.834 | 1.891 | 2.240 | 2.711 | 2.819 |
WAICを調べると、 215.6 > 211.8 で予測変数を「肉類」と「酒類」にした方を支持している。
sigmayhat^2=sigmay^2-sigmaE^2
予測値の事後分布
(13.12)式
|
|
予測値の分散の事後分布
|
|
決定係数
(13.16)式
|
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
0.759 0.051 0.641 0.666 0.766 0.831 0.841
重相関係数(決定係数の平方根に一致)
(13.14)式
(14.8)式
|
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
0.871 0.030 0.801 0.816 0.875 0.912 0.917
標準偏回帰係数
(14.7)式
肉類
|
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
0.738 0.083 0.575 0.602 0.737 0.874 0.902
酒類
|
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
0.256 0.082 0.093 0.120 0.256 0.390 0.418
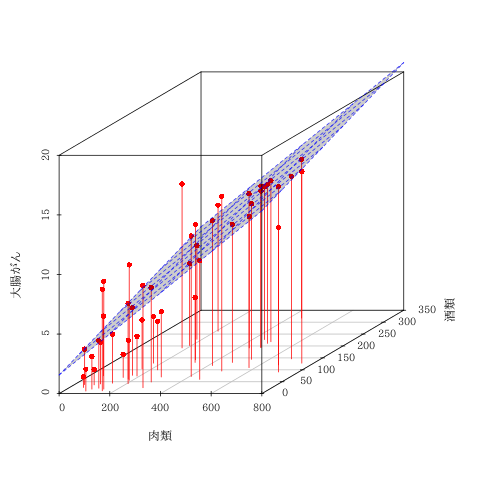
回帰平面
|
|
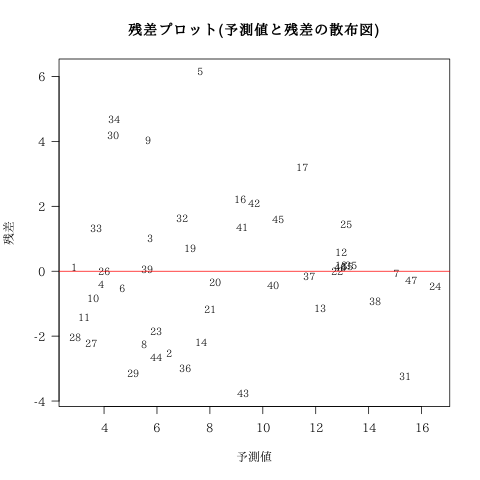
残差プロット
残差の点推定値
|
|
予測分布
(13.17)式
任意の点(テキストP.235)の事後分布・予測分布
|
|
| EAP | post.sd | 事後分布95%点 | sd | 予測分布95%点 | |
|---|---|---|---|---|---|
| 肉類0_酒類0 | 1.6 | 0.7 | 2.7 | 2.4 | 5.5 |
| 肉類300_酒類0 | 6.7 | 0.6 | 7.8 | 2.4 | 10.6 |
| 肉類0_酒類100 | 3.1 | 0.7 | 4.2 | 2.4 | 7.0 |
| 肉類150_酒類50 | 4.9 | 0.5 | 5.7 | 2.3 | 8.7 |