放送大学

心理統計法('17) その11

放送大学「心理統計法(‘17)」第13章

授業ではrstanパッケージを使ってますが、MCMCpackパッケージを使ってみます。初学者ですので間違いが多々あると思います。

（Rスクリプトはここ）
早稲田大学文学部文学研究科 豊田研究室

（参考）
ベイジアンMCMCによる統計モデル
Using the ggmcmc package
Bayesian Inference With Stan ~番外編~
Exercise 2: Bayesian A/B testing using MCMC Metropolis-Hastings
政治学方法論 I

データ
Smoking and Cancer 

1
2
3
4
5
6
7
8
9
10
11
12
13
#表13.1 「肺がんデータ」入力
STATE<-c("AK","AL","AR","AZ","CA","CT","DC","DE","FL","ID","IL","IN","IO","KS","KY","LA","MA","MD","ME","MI","MN","MO","MS","MT","NB","ND","NE","NJ","NM","NY","OH","OK","PE","RI","SC","SD","TE","TX","UT","VT","WA","WI","WV","WY")
CIG<-c(30.34,18.2,18.24,25.82,28.6,31.1,40.46,33.6,28.27,20.1,27.91,26.18,22.12,21.84,23.44,21.58,26.92,25.91,28.92,24.96,22.06,27.56,16.08,23.75,23.32,19.96,42.4,28.64,21.16,29.14,26.38,23.44,23.78,29.18,18.06,20.94,20.08,22.57,14,25.89,21.17,21.25,22.86,28.04)
LUNG<-c(25.88,17.05,15.98,19.8,22.07,22.83,27.27,24.55,23.57,13.58,22.8,20.3,16.59,16.84,17.71,25.45,22.04,26.48,20.94,22.72,14.2,20.98,15.6,19.5,16.7,12.12,23.03,25.95,14.59,25.02,21.89,19.45,12.11,23.68,17.45,14.11,17.6,20.74,12.01,21.22,20.34,20.55,15.53,15.92)
#
smoke <- data.frame(STATE,CIG,LUNG)
#
#png("sinri13_01.png")
#par(family="TakaoExMincho")
plot(smoke$CIG, smoke$LUNG,type="n",xlab="喫煙数",ylab="肺がん",xlim=c(10,50),ylim=c(10,30))
text(smoke$CIG, smoke$LUNG,smoke$STATE,cex=0.8)
title("喫煙数と肺がん")
#dev.off()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
library(MCMCpack)
library(knitr)
#
fun <- function(beta, x ,y ) {
# 切片 : beta[1] , 傾き : beta[2] , sigmaE : beta[3]
	ifelse (beta[3] < 0,l <- -Inf,
	 {
		e <- y - (beta[1] + beta[2] * x)
		l <- sum(log(dnorm(e, 0, beta[3])))
	}
	)
	return(l)
}
#
chains  <- 1:5
seeds  <- seq(1,5,1)
burnin<-2000
mcmc_n<-200000
thin<- verbose <-10
#sink("./likelihood.txt")
blm <- lapply(chains ,
			function(chain) {
				MCMCmetrop1R(fun = fun ,
				theta.init = c(1,1,1) ,
				burnin = burnin, mcmc = mcmc_n ,thin=thin,
#				verbose= verbose,
				seed = seeds[chain], logfun=TRUE ,
				x=smoke$CIG ,y=smoke$LUNG  )})
# sink()
# system("gawk '/function value/' ./likelihood.txt | gawk 'gsub(\"function value =\",\"\")' > ./lik.txt")
# l<-scan("./lik.txt")
# ll<-matrix(l,ncol=length(chains),byrow = FALSE)
# head(ll) ; tail(ll)
# lll<-ll[-c(1 : burnin/thin),]
# ( waic1 <- waic(matrix(lll,ncol=1)) )
#
blm.mcmc <- mcmc.list(blm)
#
summary(blm.mcmc)
#
gelman.diag(blm.mcmc)
#
effectiveSize(blm.mcmc)
#
df <- data.frame(a=unlist(blm.mcmc[,1]),b=unlist(blm.mcmc[,2]) ,sigmaE=unlist(blm.mcmc[,3]))
#
ryou<-rbind(EAP=apply(df, 2, mean),post.sd=apply(df, 2, sd),
	apply(df, 2, quantile, probs=c(0.025,0.05, 0.5,0.95, 0.975)))
colnames(ryou)<-c("a(切片)","b(回帰係数)","sigmaE(誤差sd)")
kable(t(round(ryou,3)))
EAP post.sd 2.5% 5% 50% 95% 97.5%
a(切片) 6.474 2.224 2.100 2.820 6.479 10.112 10.853
b(回帰係数) 0.529 0.087 0.358 0.386 0.529 0.672 0.700
sigmaE(誤差sd) 3.161 0.357 2.556 2.636 3.129 3.794 3.949

予測値の事後分布

1
2
3
4
5
6
7
yhat<-data.frame(df$a+df$b*smoke$CIG[1])
for (i in 2:nrow(smoke)){
	temp<-data.frame(df$a+df$b*smoke$CIG[i])
	yhat<-cbind(yhat,temp)
}
colnames(yhat)<-c(paste0("yhat",(1:44)))
#head(yhat)

予測値の分散の事後分布

1
sigmayhat2<-apply(yhat,1,var)

決定係数

(13.16)式

1
2
3
4
5
6
eta2<-sigmayhat2/(sigmayhat2+df$sigmaE^2)
#
ryou<-cbind(ryou,c(EAP=mean(eta2),post.sd=sd(eta2),
	quantile(eta2, probs=c(0.025,0.05, 0.5,0.95, 0.975))))
colnames(ryou)<-c("a(切片)","b(回帰係数)","sigmaE(誤差sd)","eta2")
kable(t(round(ryou,3)))
EAP post.sd 2.5% 5% 50% 95% 97.5%
a(切片) 6.474 2.224 2.100 2.820 6.479 10.112 10.853
b(回帰係数) 0.529 0.087 0.358 0.386 0.529 0.672 0.700
sigmaE(誤差sd) 3.161 0.357 2.556 2.636 3.129 3.794 3.949
eta2 0.464 0.097 0.254 0.292 0.471 0.611 0.631

事後予測分布

(13.17)式

1
2
3
4
5
6
7
yaste<-data.frame(rnorm(n = nrow(df), mean =df$a+df$b*smoke$CIG[1], sd = df$sigmaE))
for (i in 2:nrow(smoke)){
	temp<-data.frame(rnorm(n = nrow(df), mean =df$a+df$b*smoke$CIG[i], sd = df$sigmaE))
	yaste<-cbind(yaste,temp)
}
colnames(yaste)<-c(paste0("yaste",(1:44)))
#head(yaste)

残差

1
2
3
4
5
6
zansa<-data.frame(smoke$LUNG[1] - yhat[,1])
for (i in 2:ncol(yhat)){
	temp<-data.frame(smoke$LUNG[i] - yhat[,i])
	zansa<-cbind(zansa,temp)
}
colnames(zansa)<-c(paste0("zansa",(1:ncol(yhat))))

残差の点推定値

1
2
3
4
5
6
7
8
9
10
11
eihat<-smoke$LUNG - apply(yhat,2,mean)
#
#
#png("sinri13_2.png")
#par(family="TakaoExMincho")
#plot(smoke$CIG,apply(zansa,2,mean),type="n") 
plot(smoke$CIG,eihat,type="n",las=1,xlab="喫煙数",ylab="残差") 
text(smoke$CIG,eihat,smoke$STATE,cex=0.8)
title("喫煙数と肺がん(残差プロット)")
abline(h=0,col="red",lwd=1)
#dev.off()

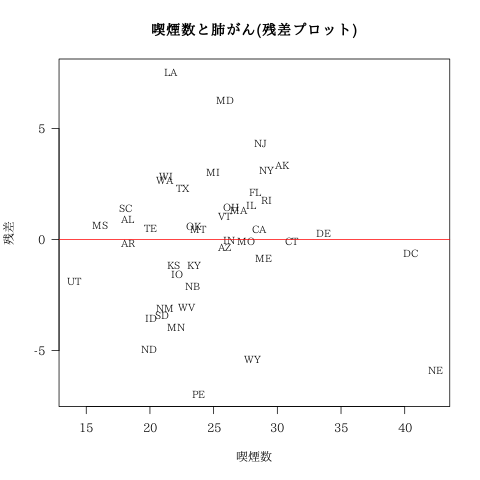
回帰直線

任意の予測変数の事後分布

(13.13)式

8から52まで2つおき

1
2
3
4
5
6
7
8
c<-seq(8,52,2)
#
yz1<-data.frame(df$a+df$b*c[1])
for (i in 2:length(c)){
	temp<-data.frame(df$a+df$b*c[i])
	yz1<-cbind(yz1,temp)
}
colnames(yz1)<-c(paste0("yz",(1:length(c))))

任意の予測変数の事後予測分布

(13.18)式

8から52まで2つおき

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
c<-seq(8,52,2)
#
yz2<-data.frame(rnorm(n = nrow(df), mean =df$a+df$b*c[1], sd = df$sigmaE))
for (i in 2:length(c)){
	temp<-data.frame(rnorm(n = nrow(df), mean =df$a+df$b*c[i], sd = df$sigmaE))
	yz2<-cbind(yz2,temp)
}
colnames(yz2)<-c(paste0("yz",(1:length(c))))
#
#
#png("sinri13_3.png")
#par(family="TakaoExMincho")
plot(smoke$CIG, smoke$LUNG,type="p",pch=20,xlab="喫煙数",ylab="肺がん",xlim=c(10,50),ylim=c(10,30),las=1)
abline(mean(df$a),mean(df$b),col="red",lwd=2)
lines(c,apply(yz1,2,quantile,probs=c(0.025)),col="blue")
lines(c,apply(yz1,2,quantile,probs=c(0.975)),col="blue")
lines(c,apply(yz2,2,quantile,probs=c(0.025)),col="green",lty=2)
lines(c,apply(yz2,2,quantile,probs=c(0.975)),col="green",lty=2)
title("確信区間と予測区間")
#dev.off()

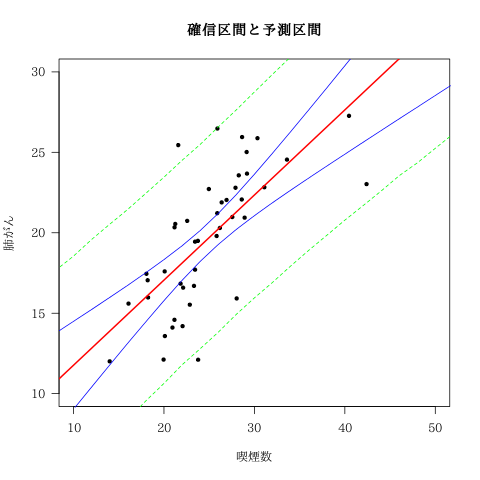
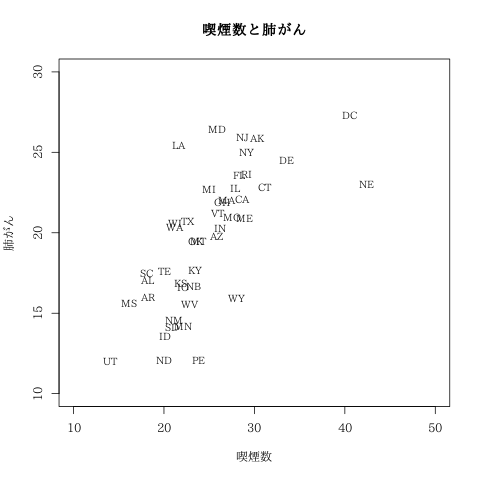
　予測値・残差・事後標準偏差・確信区間・予測区間

州名 : smoke$STATE , 予測値の事後分布 : yhat , 事後予測分布 : yaste , 残差 : eihat

1
2
3
4
5
6
7
8
res<-data.frame(apply(yhat,2,mean),eihat,apply(yhat,2,sd),apply(yhat,2,quantile, probs=0.025),
	apply(yhat,2,quantile, probs=0.975),apply(yaste,2,sd),apply(yaste,2,quantile, probs=0.025),
	apply(yaste,2,quantile, probs=0.975))
#
rownames(res)<-smoke$STATE
colnames(res)<-c("予測値","残差","post.sd","確信95%(下)","確信95%(上)","sd","予測95%(下)","予測95%(上)")
#
kable(round(res,2))
予測値 残差 post.sd 確信95%(下) 確信95%(上) sd 予測95%(下) 予測95%(上)
AK 22.53 3.35 0.67 21.20 23.86 3.23 16.14 28.88
AL 16.10 0.95 0.76 14.60 17.60 3.27 9.70 22.54
AR 16.12 -0.14 0.76 14.63 17.61 3.27 9.67 22.59
AZ 20.13 -0.33 0.49 19.18 21.10 3.21 13.83 26.46
CA 21.60 0.47 0.58 20.47 22.75 3.23 15.20 27.93
CT 22.93 -0.10 0.72 21.51 24.35 3.25 16.52 29.24
DC 27.88 -0.61 1.43 25.05 30.70 3.48 21.06 34.75
DE 24.25 0.30 0.89 22.49 26.01 3.30 17.76 30.74
FL 21.43 2.14 0.56 20.33 22.54 3.24 15.06 27.81
ID 17.11 -3.53 0.64 15.84 18.37 3.24 10.74 23.49
IL 21.24 1.56 0.55 20.17 22.32 3.23 14.90 27.59
IN 20.32 -0.02 0.49 19.36 21.30 3.23 13.97 26.68
IO 18.18 -1.59 0.54 17.11 19.24 3.21 11.84 24.47
KS 18.03 -1.19 0.55 16.94 19.12 3.22 11.70 24.44
KY 18.87 -1.16 0.50 17.90 19.86 3.22 12.52 25.23
LA 17.89 7.56 0.56 16.78 19.00 3.23 11.54 24.25
MA 20.72 1.32 0.51 19.71 21.72 3.23 14.36 27.13
MD 20.18 6.30 0.49 19.22 21.15 3.22 13.84 26.47
ME 21.77 -0.83 0.59 20.61 22.95 3.24 15.34 28.16
MI 19.68 3.04 0.48 18.74 20.63 3.20 13.33 25.98
MN 18.14 -3.94 0.54 17.08 19.21 3.23 11.81 24.48
MO 21.05 -0.07 0.53 20.01 22.11 3.23 14.73 27.45
MS 14.98 0.62 0.91 13.19 16.77 3.30 8.47 21.50
MT 19.04 0.46 0.49 18.08 20.01 3.22 12.74 25.39
NB 18.81 -2.11 0.50 17.83 19.80 3.22 12.46 25.16
ND 17.03 -4.91 0.65 15.75 18.31 3.25 10.60 23.38
NE 28.91 -5.88 1.59 25.76 32.04 3.57 21.90 35.99
NJ 21.63 4.32 0.58 20.49 22.77 3.24 15.24 28.01
NM 17.67 -3.08 0.58 16.52 18.82 3.24 11.29 24.05
NY 21.89 3.13 0.60 20.70 23.09 3.23 15.50 28.28
OH 20.43 1.46 0.50 19.46 21.41 3.22 14.11 26.79
OK 18.87 0.58 0.50 17.90 19.86 3.22 12.52 25.21
PE 19.05 -6.94 0.49 18.09 20.03 3.21 12.72 25.37
RI 21.91 1.77 0.61 20.72 23.11 3.24 15.51 28.25
SC 16.03 1.42 0.77 14.51 17.54 3.27 9.61 22.45
SD 17.55 -3.44 0.60 16.38 18.73 3.24 11.15 23.93
TE 17.10 0.50 0.64 15.83 18.36 3.24 10.69 23.50
TX 18.41 2.33 0.52 17.39 19.45 3.23 12.07 24.77
UT 13.88 -1.87 1.07 11.78 15.98 3.36 7.27 20.50
VT 20.17 1.05 0.49 19.21 21.14 3.22 13.85 26.49
WA 17.67 2.67 0.58 16.52 18.83 3.23 11.26 24.02
WI 17.72 2.83 0.58 16.57 18.86 3.24 11.30 24.05
WV 18.57 -3.04 0.52 17.56 19.58 3.21 12.20 24.86
WY 21.31 -5.39 0.55 20.22 22.40 3.23 14.94 27.66