放送大学「心理統計法(‘17)」第3章 第4章
授業ではrstanパッケージを使ってますが、MCMCpackパッケージを使ってみます。初学者ですので間違いが多々あると思います。
(Rスクリプトはここ)
早稲田大学文学部文学研究科 豊田研究室
ダウンロードしてすべてのスクリプトを実行してみました。
(最初の結果が出るのに時間がかかりますが、結果を保存しておけば2回目からは快適です。)
(参考)
ベイジアンMCMCによる統計モデル
Using the ggmcmc package
Bayesian Inference With Stan ~番外編~
Exercise 2: Bayesian A/B testing using MCMC Metropolis-Hastings
政治学方法論 I
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
| library(MCMCpack) library(ggmcmc) library(knitr) #表1.1の「知覚時間」のデータ入力 x<-c(31.43,31.09,33.38,30.49,29.62, 35.40,32.58,28.96,29.43,28.52, 25.39,32.68,30.51,30.15,32.33, 30.43,32.50,32.07,32.35,31.57) #MCMC推定に使用する関数を用意する。 #betaは要素数2のベクトル。 #beta[1]が平均、beta[2]が標準偏差で、betaを推定する。 #関数の返り値は対数尤度。標準偏差は非負なので、0か負になったときは対数尤度をマイナス無限大とする。 # llnormfun <- function(beta, x) { ifelse (beta[2] < 0, l<- -Inf, l <- sum(log(dnorm(x, mean=beta[1], sd=beta[2])))) return(l) }
|
繰り返し3000回、初期値依存として捨てる数を0として、MCMC推定を実行。( chain=5 )
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| post1 <- MCMCmetrop1R(llnormfun, theta.init = c(0, 30), x = x, mcmc = 3000, burnin=0,seed =1) post2 <- MCMCmetrop1R(llnormfun, theta.init = c(0, 30), x = x, mcmc = 3000, burnin=0,seed =2) post3 <- MCMCmetrop1R(llnormfun, theta.init = c(0, 30), x = x, mcmc = 3000, burnin=0,seed =3) post4 <- MCMCmetrop1R(llnormfun, theta.init = c(0, 30), x = x, mcmc = 3000, burnin=0,seed =4) post5 <- MCMCmetrop1R(llnormfun, theta.init = c(0, 30), x = x, mcmc = 3000, burnin=0,seed =5) geweke.diag(post1)
|
Fraction in 1st window = 0.1
Fraction in 2nd window = 0.5
var1 var2
-2.792 18.457
1 2 3 4
| posterior <- mcmc.list(post1, post2, post3, post4, post5) #png("bayes3_1.png") plot(posterior, trace = TRUE, density = TRUE) #dev.off()
|
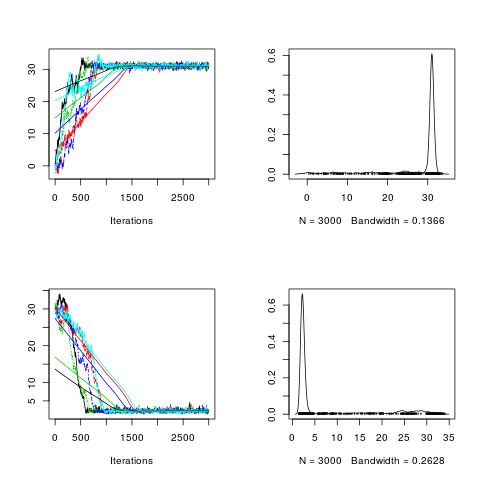
Iterations = 1:3000
Thinning interval = 1
Number of chains = 5
Sample size per chain = 3000
Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
[1,] 27.648 7.722 0.06305 1.738
[2,] 7.023 9.127 0.07452 2.810
Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
[1,] 2.491 30.085 30.862 31.27 32.09
[2,] 1.694 2.097 2.403 4.37 30.10
Potential scale reduction factors:
Point est. Upper C.I.
[1,] 1.01 1.01
[2,] 1.01 1.03
Multivariate psrf
1.01
1
| effectiveSize(posterior)
|
var1 var2
28.46518 11.41829
1500回くらいまでは収束していない。(rstanはずっと早く収束する)
effectiveSizeも3000回*5=15000回で28 、 11
繰り返し20000回、初期値依存として捨てる数を2000として、MCMC推定を実行。( chain=5 )
lapply()関数を使ってプログラムを短く
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
| chains <- 1:5 seeds <- seq(1,5,1) posterior2 <- lapply(chains , function(chain) { MCMCmetrop1R(fun = llnormfun , theta.init = c(0,30), burnin = 2000, mcmc = 20000, seed = seeds[chain],thin=1, x = x)}) #class(posterior2) #str(posterior2) #geweke.diag(posterior2[[1]]) post2.mcmc <- mcmc.list(posterior2) #png("bayes3_2.png") plot(post2.mcmc, trace = TRUE, density = TRUE) #dev.off()
|
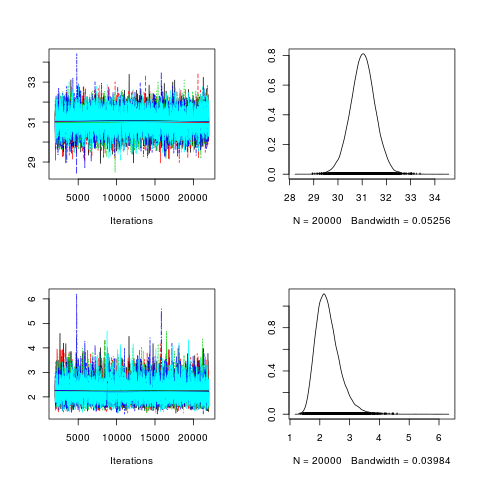
Iterations = 2001:22000
Thinning interval = 1
Number of chains = 5
Sample size per chain = 20000
Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
[1,] 31.028 0.5133 0.001623 0.005449
[2,] 2.274 0.4033 0.001275 0.005282
Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
[1,] 29.999 30.696 31.031 31.361 32.034
[2,] 1.652 1.991 2.221 2.495 3.216
Potential scale reduction factors:
Point est. Upper C.I.
[1,] 1 1
[2,] 1 1
Multivariate psrf
1
1
| effectiveSize(post2.mcmc)
|
var1 var2
8876.217 5971.989
effectiveSize : 20000回*5=100000回で8876, 5972
繰り返し200000回、初期値依存として捨てる数を2000、thin(サンプルを得る間隔)=10として、MCMC推定を実行。( chain=5 )
1 2 3 4 5 6 7 8 9 10 11 12 13
| chains <- 1:5 seeds <- seq(1,5,1) posterior3 <- lapply(chains , function(chain) { MCMCmetrop1R(fun = llnormfun , theta.init = c(0,30), burnin = 2000, mcmc = 200000, seed = seeds[chain],thin=10, x = x)}) post3.mcmc <- mcmc.list(posterior3) plot(post3.mcmc, trace = TRUE, density = TRUE)
|
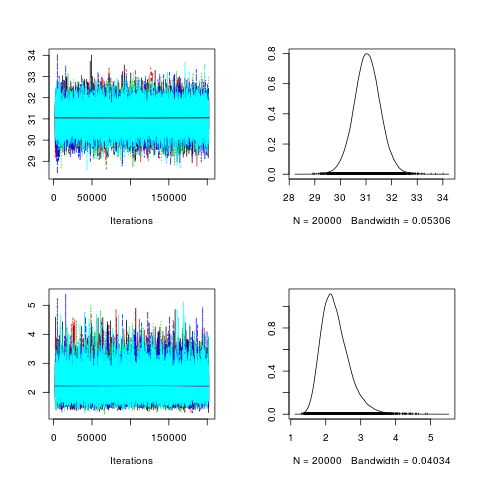
Iterations = 2001:201991
Thinning interval = 10
Number of chains = 5
Sample size per chain = 20000
Empirical mean and standard deviation for each variable,
plus standard error of the mean:
Mean SD Naive SE Time-series SE
[1,] 31.047 0.5173 0.001636 0.001998
[2,] 2.275 0.4048 0.001280 0.001768
Quantiles for each variable:
2.5% 25% 50% 75% 97.5%
[1,] 30.028 30.71 31.045 31.38 32.078
[2,] 1.647 1.99 2.219 2.50 3.222
Potential scale reduction factors:
Point est. Upper C.I.
[1,] 1 1
[2,] 1 1
Multivariate psrf
1
1
| effectiveSize(post3.mcmc)
|
var1 var2
67206.95 52591.34
effectiveSize : 20000回*5=100000回で67207 , 52591
ほぼテキスト並の数値になったので以後はこの出力を使う
xasteは、推定されたsigma を使って正規分布から無作為に抽出する必要がある。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
| df <- data.frame(mu=unlist(post3.mcmc[,1]),sigma=unlist(post3.mcmc[,2])) xaste<-rnorm(n = nrow(df), mean =df$mu, sd = df$sigma) # df<- data.frame(df,xaste) # # kanitr::kableを使って出力を工夫 # ryou<-data.frame(c(round(mean(df[,1]),2) , round(sd(df[,1]),2) , round(quantile(df[,1],c(0.025,0.05,0.5,0.95,0.975)),2))) for (i in 2:ncol(df) ){ ryou<-cbind(ryou,data.frame(c(round(mean(df[,i]),2) , round(sd(df[,i]),2) , round(quantile(df[,i],c(0.025,0.05,0.5,0.95,0.975)),2)))) } names(ryou)<-c("mu","sigma","xaste") rownames(ryou)<-c("EAP","post.sd","2.5%","5%","50%","95%","97.5%") # kable(t(ryou))
|
|
EAP |
post.sd |
2.5% |
5% |
50% |
95% |
97.5% |
| mu |
31.05 |
0.52 |
30.03 |
30.20 |
31.04 |
31.90 |
32.08 |
| sigma |
2.28 |
0.40 |
1.65 |
1.72 |
2.22 |
3.02 |
3.22 |
| xaste |
31.04 |
2.36 |
26.37 |
27.18 |
31.04 |
34.89 |
35.70 |
1 2 3 4 5
| #png() hist(df$xaste,breaks=100,main=) #abline(v=mean(df$xaste),col=) segments(mean(df$xaste),0,mean(df$xaste),par()[4],lwd=2.5 ,col=) #dev.off()
|
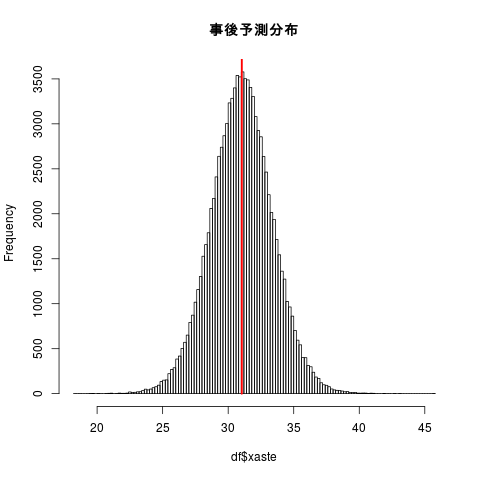
1 2 3 4 5 6 7 8 9 10 11 12
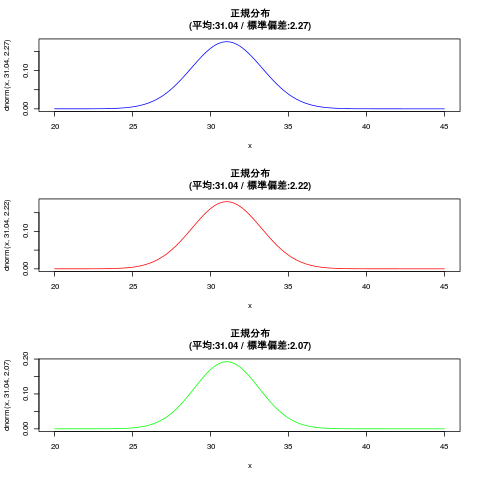
| # 確率密度関数(dnorm): 確率分布関数(pnorm)とその逆関数(qnorm) x<-seq(20,45,0.1) #png("bayes3_8.png") par(mfrow=c(3,1)) curve(dnorm(x,31.04,2.27),20,45, col="blue") title(main="正規分布\n(平均:31.04 / 標準偏差:2.27)") curve(dnorm(x,31.04,2.22),20,45, col="red") title(main="正規分布\n(平均:31.04 / 標準偏差:2.22)") curve(dnorm(x,31.04,2.07),20,45, col="green") title(main="正規分布\n(平均:31.04 / 標準偏差:2.07)") par(mfrow=c(1,1)) #dev.off()
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
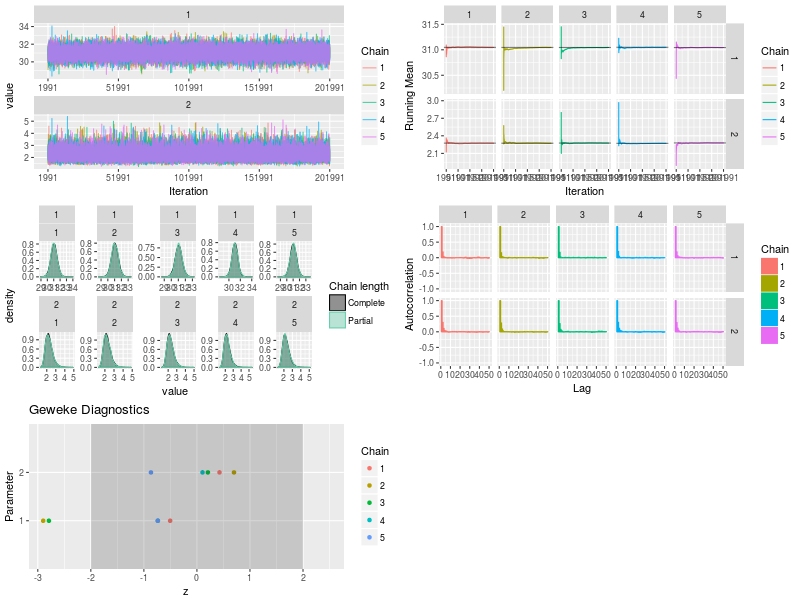
| library(ggmcmc) #ggmcmc(ggs(post3.mcmc), file="posterior.pdf") #ggmcmc(ggs(post3.mcmc), plot=c("histogram", "traceplot", "geweke")) #ggmcmc(ggs(post3.mcmc), plot=c("histogram"),file=NULL) #ggs_histogram(ggs(post3.mcmc)) #ggs_density(ggs(post3.mcmc)) #ggs_traceplot(ggs(post3.mcmc)) #ggs_running(ggs(post3.mcmc)) #ggs_compare_partial(ggs(post3.mcmc)) #ggs_autocorrelation(ggs(post3.mcmc)) #ggs_crosscorrelation(ggs(post3.mcmc)) #ggs_Rhat(ggs(post3.mcmc)) + xlab("R_hat") #ggs_geweke(ggs(post3.mcmc)) # #png("bayes3_5.png",width=800,height=600) p1<-ggs_traceplot(ggs(post3.mcmc)) p2<-ggs_running(ggs(post3.mcmc)) p3<-ggs_compare_partial(ggs(post3.mcmc)) p4<-ggs_autocorrelation(ggs(post3.mcmc)) p5<-ggs_geweke(ggs(post3.mcmc)) gridExtra::grid.arrange(p1, p2, p3, p4, p5,ncol = 2) #dev.off()
|
1 2 3 4 5 6 7
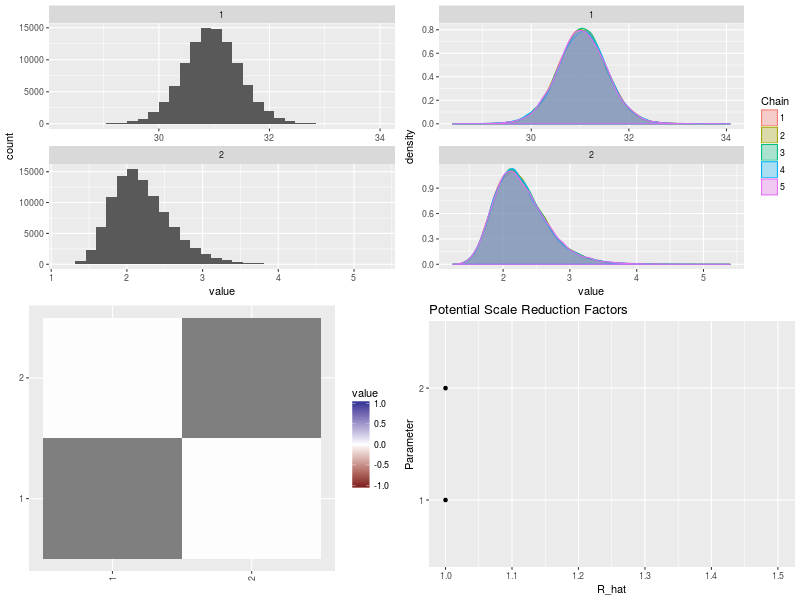
| #png("bayes3_6.png",width=800,height=600) p1<-ggs_histogram(ggs(post3.mcmc)) p2<-ggs_density(ggs(post3.mcmc)) p3<-ggs_crosscorrelation(ggs(post3.mcmc)) p4<-ggs_Rhat(ggs(post3.mcmc)) + xlab("R_hat") gridExtra::grid.arrange(p1, p2, p3, p4,ncol = 2) #dev.off()
|
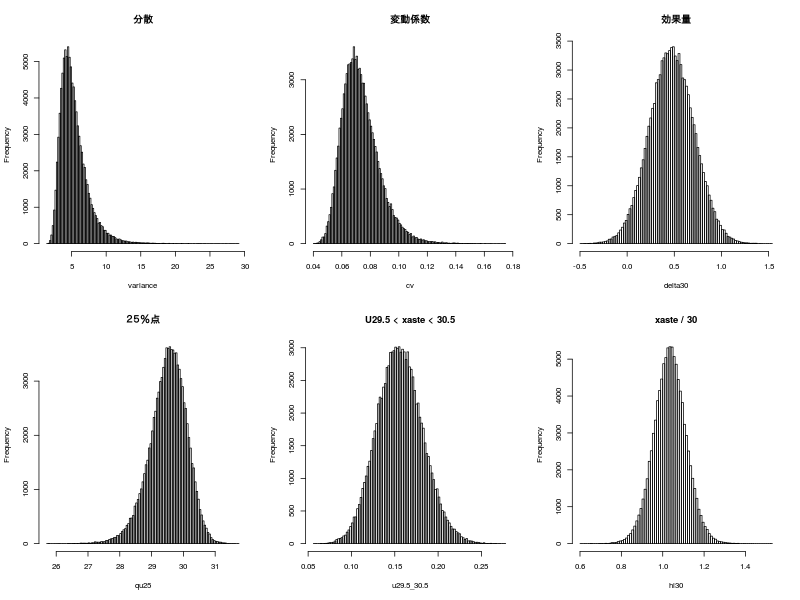
p.61 生成量の推定結果
分散
1 2 3
| variance <- df$sigma^2 c(EAP=round(mean(variance),3) , post.sd=round(sd(variance),3) , round(quantile(variance,c(0.025,0.05,0.5,0.95,0.975)),3))
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
5.340 2.018 2.712 2.964 4.922 9.102 10.378
変動係数
1 2 3
| cv<- df$sigma/df$mu c(EAP=round(mean(cv),3) , post.sd=round(sd(cv),3) , round(quantile(cv,c(0.025,0.05,0.5,0.95,0.975)),3))
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
0.073 0.013 0.053 0.055 0.071 0.097 0.104
効果量
1 2 3 4
| c<-30 delta30<- (df$mu-c)/df$sigma c(EAP=round(mean(delta30),3) , post.sd=round(sd(delta30),3) , round(quantile(delta30,c(0.025,0.05,0.5,0.95,0.975)),3))
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
0.474 0.237 0.012 0.085 0.473 0.865 0.939
分位点・%点
1 2 3 4
| z<-qnorm(0.25, mean=0, sd=1) qu25<- df$mu + z * df$sigma c(EAP=round(mean(qu25),3) , post.sd=round(sd(qu25),3) , round(quantile(qu25,c(0.025,0.05,0.5,0.95,0.975)),3))
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
29.513 0.583 28.246 28.495 29.552 30.390 30.540
特定区間での観測確率
1 2 3
| u29.5_30.5<-pnorm(30.5, mean =df$mu, sd = df$sigma)-pnorm(29.5, mean =df$mu, sd = df$sigma) c(EAP=round(mean(u29.5_30.5),3) , post.sd=round(sd(u29.5_30.5),3) , round(quantile(u29.5_30.5,c(0.025,0.05,0.5,0.95,0.975)),3))
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
0.156 0.026 0.106 0.114 0.155 0.201 0.210
比の分布
1 2 3 4
| c<-30 hi30<-df$xaste/c c(EAP=round(mean(hi30),3) , post.sd=round(sd(hi30),3) , round(quantile(hi30,c(0.025,0.05,0.5,0.95,0.975)),3))
|
EAP post.sd 2.5% 5% 50% 95% 97.5%
1.035 0.079 0.879 0.906 1.035 1.163 1.190
各種事後分布
1 2 3 4 5 6 7 8 9 10
| par(mfrow=c(2,3)) hist(variance,breaks=100,main="分散") hist(cv,breaks=100,main="変動係数") hist(delta30,breaks=100,main="効果量") hist(qu25,breaks=100,main="25%点") hist(u29.5_30.5,breaks=100,main="U29.5 < xaste < 30.5") hist(hi30,breaks=100,main="xaste / 30") par(mfrow=c(1,1))
|
研究仮説が正しい確率
30<mu
1 2
| p<-table(df$mu > 30) p[2]/(p[1]+p[2])
|
TRUE
0.9778
29.5<mu<30.5
1 2
| p<-table(df$xaste > 29.5 & df$xaste < 30.5) p[2]/(p[1]+p[2])
|
TRUE
0.15509
delta30 > 0.5
1 2
| p<-table(delta30 > 0.5) p[2]/(p[1]+p[2])
|
TRUE
0.45327
29.5 < 測定値 < 30.5 の確率が20%未満の確率
1 2
| p<- table(u29.5_30.5 < 0.2) p[2]/(p[1]+p[2])
|
TRUE
0.94793
本格的にやるには「rstan」でしょうけど、ベイズ統計初学者には「rstan」より「MCMCpack」の方がとっつきやすいのでは。







